第3回：逐次的なPythonへの移植と露呈するパフォーマンス問題

前回までの作業で、移植対象のFortranコード dsvdc.f90 の課題を特定し（第1回）、GOTO文の構造化と0ベース配列化というリファクタリングを完了しました（第2回）。これにより、Pythonへの移植を妨げる主要な技術的障壁が取り除かれ、より機械的な構文変換作業に集中できる環境が整いました。

本稿では、このリファクタリング済みFortranコードをPythonに移植する実際のプロセスを報告します。さらに、移植が完了したコードのパフォーマンスを実測し、オリジナルのFortran版と比較することで明確になった課題についても述べます。

安全性を優先する移植アプローチ

FortranからPythonへコードを書き換える際、よりPythonらしい効率的なコード（Pythonicなコード）への大幅なリファクタリングも選択肢の一つです。 しかし今回は、そうしたアプローチではなく、まずはFortranのロジックをそのままPythonに直訳的に置き換える保守的な手法を採用しました。

段階的移植戦略の全体像

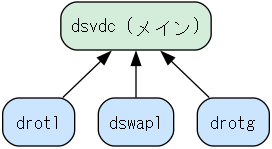
1. ボトムアップでの移植順序 依存関係を考慮し、他のサブルーチンから呼び出されるヘルパー関数から移植を開始しました。具体的にはdrot1、dswap1、drotgを先に移植し、最後にこれらを呼び出すメインのdsvdcを移植しました。

2. 正解データを使った検証 各サブルーチンについて、Fortran版での実際の入力データと出力値を正解データとして記録し、Python版での移植実装後に記録したデータを使った単体テストを実施しました。一つのサブルーチンでこの一連の作業を完了してから次に進むことで、確実性を保ちました。

3. 統合テスト 全サブルーチンの単体テストが完了後、システム全体でFortran版と同一の最終出力が得られることを確認しました。

各サブルーチンでの詳細作業手順

前述の戦略に基づき、各サブルーチンでは以下の3つのステップを順番に実行する形で作業を進めました。

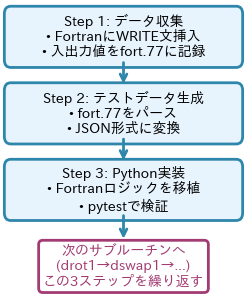
Step 1: 対象サブルーチンでのFortran入出力データ収集

まず、移植対象のFortranサブルーチンが、テスト実行時にどのような入力値を受け取り、どのような出力値を返しているかを記録しました。

そのために、対象サブルーチンのコードに一時的な変更を加え、エントリーポイント直後に入力引数の値を、リターン直前に出力引数の値を、特定のファイルに書き出すWRITE文を挿入しました。

ログ出力には、固定の装置番号を使用しました（今回は77）が、これは、OPEN文やCLOSE文、あるいは動的な装置番号割り当て(NEWUNIT)といった管理の複雑さを避けるためです。

以下は、ヘルパー関数 drot1 にログ出力コードを挿入した際の例です。

! SVDモジュール内のサブルーチン drot1 へのログ出力追加例
SUBROUTINE drot1 (n_arg, dx_arr, dy_arr, c_val, s_val)
  IMPLICIT NONE
  INTEGER, INTENT(IN)      :: n_arg
  REAL (dp), INTENT(IN OUT) :: dx_arr(0:*)
  REAL (dp), INTENT(IN OUT) :: dy_arr(0:*)
  REAL (dp), INTENT(IN)      :: c_val, s_val
  INTEGER                   :: i_log_local

  ! ▼▼▼ 挿入したログ出力コード (入口) ▼▼▼
  WRITE(77, '(A)') "--- drot1 Entry (using unit 77) ---"
  WRITE(77, '(A, I0)') "N_arg = ", n_arg
  WRITE(77, '(A, ES22.14E3)') "C_val = ", c_val
  ! ... (他の入力引数も同様に書き出す) ...

  ! ===== オリジナルのdrot1ロジック (変更なし) =====
  
  ! ▼▼▼ 挿入したログ出力コード (出口) ▼▼▼
  DO i_log_local = 0, n_arg - 1
    WRITE(77, '(A,A,I0,A,ES22.14E3)') 'DX_arr_OUT[', i_log_local, '] = ', dx_arr(i_log_local)
  END DO
  DO i_log_local = 0, n_arg - 1
    WRITE(77, '(A,A,I0,A,ES22.14E3)') 'DY_arr_OUT[', i_log_local, '] = ', dy_arr(i_log_local)
  END DO
  WRITE(77, '(A)') "--- drot1 Exit (using unit 77) ---"
END SUBROUTINE drot1

このログ出力コードを埋め込んだFortranプログラムを実行すると、fort.77 というファイルに対象サブルーチンの全呼び出しにおける入出力データが時系列で記録されます。

Fortranから出力された実際のログデータ例（fort.77の一部）:

--- drot1 Entry (using unit 77) ---
N_arg = 3
C_val = -5.07476807628067E-001
S_val = 8.61665416341880E-001
DX_arr_IN[0] = 1.00000000000000E+000
DX_arr_IN[1] = 0.00000000000000E+000
DX_arr_IN[2] = 0.00000000000000E+000
DY_arr_IN[0] = 0.00000000000000E+000
DY_arr_IN[1] = -6.67002248418850E-001
DY_arr_IN[2] = -7.45055703021055E-001
--- drot1 Exit (using unit 77) ---
DX_arr_OUT[0] = -5.07476807628067E-001
DX_arr_OUT[1] = -5.74732770084798E-001
DX_arr_OUT[2] = -6.41988732541530E-001
DY_arr_OUT[0] = -8.61665416341880E-001
DY_arr_OUT[1] = 3.38488171708341E-001
DY_arr_OUT[2] = 3.78098489674210E-001
  ... 複数パターンが続く

Step 2: JSON形式のテストデータ生成

次に、このログファイルをそのまま使うのではなく、Pythonのテストで扱いやすいように、簡単なPythonコードを用いて構造化されたJSON形式のデータに変換しました。

JSONファイルの構造例

[
  {
    "call_id": 1,
    "inputs": {
      "N_arg": 3,
      "C_val": -0.507476807628067,
      "S_val": 0.861665416341880,
      "DX_arr_IN": [
        1.00000000000000E+000,
        0.00000000000000E+000,
        0.00000000000000E+000
      ],
      "DY_arr_IN": [
        0.00000000000000E+000,
        -6.67002248418850E-001,
        -7.45055703021055E-001
      ]
    },
    "outputs": {
      "DX_arr_OUT": [
        -5.07476807628067E-001,
        -5.74732770084798E-001,
        -6.41988732541530E-001
      ],
      "DY_arr_OUT": [
        -8.61665416341880E-001,
        3.38488171708341E-001,
        3.78098489674210E-001
      ]
    }
  },
  ... 複数パターンが続く
]

このJSONファイルが、Python側の単体テストにおける入力値と期待される「正解の出力値」となります。

Step 3: Python関数の実装と単体テスト

対象サブルーチンの正解データが準備できたら、次はPythonへの移植作業に進みます。

全体の進行順序

ヘルパー関数（drot1, dswap1, drotg）から順に移植し、最後にそれらのヘルパー関数を呼び出しているメイン関数 dsvdc を実装しました。各関数でFortranと完全に同じ振る舞いを確認してから次に進みました。

各関数での作業手順 1. Python関数の実装: Fortranのロジックを忠実に再現したPython関数を作成 2. 単体テストの作成: pytest（Pythonのテストツール）を使い、JSON形式の正解データを読み込んでテストするコードを作成
3. 実装とテストの繰り返し: Python関数を実行し、JSONの期待値と比較検証。すべてのテストが通るまでPythonコードを修正

単体テストのコード例

dswap1 のテストコードの例（抜粋）を示します。

@pytest.mark.parametrize("test_case", load_test_data())
def test_dswap1(test_case):
    # 入力データを準備
    n = test_case["inputs"]["N_arg"]
    dx = np.array(test_case["inputs"]["DX_arr_IN"], dtype=np.float64)
    dy = np.array(test_case["inputs"]["DY_arr_IN"], dtype=np.float64)
    
    # Python関数を実行
    dswap1(n, dx, dy)
    
    # 期待値と比較検証
    expected_dx = np.array(test_case["outputs"]["DX_arr_OUT"], dtype=np.float64)
    expected_dy = np.array(test_case["outputs"]["DY_arr_OUT"], dtype=np.float64)
    np.testing.assert_allclose(dx, expected_dx, rtol=1e-7, atol=1e-9)
    np.testing.assert_allclose(dy, expected_dy, rtol=1e-7, atol=1e-9)

ここでは @pytest.mark.parametrize デコレータを用いて、すぐ下のtest_dswap1関数が複数の異なるテストケースで自動実行されるようにしています。 また、数値の比較には numpy.testing.assert_allclose を使用し、浮動小数点の計算誤差を許容範囲内として扱うようにしています。

テストコード及びデータ

今回テストで用いたコードとデータは以下よりご参照いただけます。

• テストコード：test_svd_components.py

• テスト正解データ：

  • dswap1用: dswap1_golden_master.json
  • drotg用: drotg_golden_master.json
  • drot1用: drot1_with_t_svd.json
  • dsvdc用: dsvdc_with_advanced_tester.json

具体的な移植例：単純なループから引数の挙動まで

ここまでは移植の「プロセス」に焦点を当ててきましたが、実際のコードがどのように変換されたのか、具体的な例をいくつか見てみたいと思います。ここでは、ヘルパー関数である dswap1 と drotg の移植を例に、FortranからPythonへの「直訳的」な変換がどのように行われたかを紹介します。

移植例1: dswap1 – ループと配列操作の基本

まずは、2つの配列の要素を入れ替えるシンプルなサブルーチン dswap1 を見てみます。この例では、基本的なループ構造や配列アクセスの変換方法を確認できます。

Fortran版 dswap1

SUBROUTINE dswap1 (n, dx, dy)
  INTEGER, INTENT(IN)     :: n
  REAL (dp), INTENT(IN OUT) :: dx(0:*)
  REAL (dp), INTENT(IN OUT) :: dy(0:*)

  REAL (dp)  :: dtemp
  INTEGER    :: i, m

  IF(n <= 0) RETURN
  m = MOD(n,3)
  IF (m /= 0) THEN
    DO i = 0, m-1
      dtemp = dx(i)
      dx(i) = dy(i)
      dy(i) = dtemp
    END DO
    IF( n < 3 ) RETURN 
  END IF

  DO i = m, n-1, 3
    dtemp = dx(i)
    dx(i) = dy(i)
    dy(i) = dtemp
    dtemp = dx(i + 1)
    dx(i + 1) = dy(i + 1)
    dy(i + 1) = dtemp
    dtemp = dx(i + 2)
    dx(i + 2) = dy(i + 2)
    dy(i + 2) = dtemp
  END DO
END SUBROUTINE dswap1

Python移植版 dswap1

def dswap1(n, dx, dy):
    if n <= 0:
        return

    m = n % 3 # Fortranの MOD(n,3) と同等
    if m != 0:
        for i in range(m): 
            dtemp = dx[i]
            dx[i] = dy[i]
            dy[i] = dtemp
        if n < 3:
            return
    
    # 2番目のループの開始インデックスは0ベースで m となる
    # ループ制御を0ベース化 (m から n-1 まで、ステップ3)
    for i in range(m, n, 3): 
        dtemp = dx[i]
        dx[i] = dy[i]
        dy[i] = dtemp
        
        dtemp = dx[i + 1]
        dx[i + 1] = dy[i + 1]
        dy[i + 1] = dtemp
        
        dtemp = dx[i + 2]
        dx[i + 2] = dy[i + 2]
        dy[i + 2] = dtemp

この移植は比較的簡単に行えました。前回のリファクタリングでFortranコードの配列がすべて0ベース化されていたため、Pythonの0ベースインデックスに合わせた調整は不要でした。主な作業としては、dx(i) が dx[i] に、dy(i + 1) が dy[i + 1] になるように括弧を角括弧に置き換えたり、Fortranの DO i = 0, m-1 をPythonの for i in range(m) に置き換えたり、MOD(n, 3) を剰余演算子 % に変更したりといった、基本的な構文変換が中心でした。また、引数の dx と dy はNumPy配列であり、関数内で加えた変更は呼び出し元に反映されます。これはFortranの INTENT(IN OUT) の動作と似ており、このケースでは特別な対応は必要ありませんでした。

移植例2: drotg – INTENT(IN OUT) の再現

別の例として drotg のケースを見てみます。この関数は、Fortran特有の引数の挙動、特に INTENT(IN OUT) をPythonでどう扱うかという点で、興味深い課題があります。Fortran版のdrotg は、入力引数 da と db を受け取り、計算の過程でこれらを上書きし、さらに出力引数 dc と ds に結果を格納します。

Fortran版 drotg

SUBROUTINE drotg(da, db, dc, ds)
  REAL (dp), INTENT(IN OUT)  :: da
  REAL (dp), INTENT(IN OUT)  :: db
  REAL (dp), INTENT(OUT)      :: dc
  REAL (dp), INTENT(OUT)      :: ds
  
  REAL (dp)  :: u, v, r

  IF (ABS(da) > ABS(db)) THEN
    u = da + da
    v = db / u
    r = SQRT(.25D0 + v**2) * u
    dc = da / r
    ds = v * (dc + dc)
    db = ds
    da = r
  ELSE IF (db /= 0.d0) THEN
    u = db + db
    v = da / u
    da = SQRT(.25D0 + v**2) * u ! 'da' is overwritten
    ds = db / da                 ! uses original 'db' and new 'da'
    dc = v * (ds + ds)
    IF (dc == 0.d0) THEN
      db = 1.d0
    ELSE
      db = 1.d0 / dc
    END IF
  ELSE
    dc = 1.d0
    ds = 0.d0
  END IF
END SUBROUTINE drotg

Python移植版 drotg

import math

def drotg(da_in, db_in):
    # FortranのINTENT(IN OUT)の動作を模倣するため、入力値をローカル変数にコピー
    da = float(da_in)
    db = float(db_in)
    # INTENT(OUT)の変数を初期化
    dc = 0.0
    ds = 0.0
    
    if abs(da) > abs(db):
        u = da + da
        v = db / u
        r_val = math.sqrt(0.25 + v**2) * u
        dc = da / r_val
        ds = v * (dc + dc)
        # 更新後の値を戻り値として扱う
        db = ds 
        da = r_val
    elif db != 0.0:
        u = db + db
        v = da / u
        r_val_for_da = math.sqrt(0.25 + v**2) * u
        original_db_val = db
        da = r_val_for_da
        ds = original_db_val / da
        dc = v * (ds + ds)
        if dc == 0.0:
            db = 1.0
        else:
            db = 1.0 / dc
    else:
        dc = 1.0
        ds = 0.0
        
    return da, db, dc, ds

drotg の移植では、いくつかの判断が必要でした。

• 引数の扱いと戻り値による更新: Pythonの数値型（floatやint）は変更不能なため、関数内で引数に再代入しても呼び出し元の変数は変わりません。これはFortranの INTENT(IN OUT) の動作とは異なります。

   この挙動の差を吸収し、Fortranのロジックを正確に再現するため、Python版では以下の設計を採用しました。

   1.  入力専用の引数（例: da_in, db_in）で値を受け取る。        2.  関数冒頭で、これらの値を計算用のローカル変数 da, db にコピーする。        3.  Fortranのロジックに従い、ローカル変数 da, db を変更・更新する。        4.  関数の最後に、更新後の da, db と計算結果の dc, ds をタプルとして return する。

   このように、Fortranが引数の直接更新で実現していた処理を、Pythonでは関数の戻り値で代替することで、サブルーチン呼び出しによって変数が更新されるという、元の振る舞いと同等の結果が得られるようにしました。

システム全体での動作確認

個別のサブルーチンの移植が完了した後、システム全体としての動作確認を行いました。第1回で紹介したAlan Miller氏は、dsvdc.f90と合わせて、これをテストするためのシンプルなプログラム t_svd.f90 も公開しています。このテストプログラムは以下のような4×3行列に対してSVDを実行するものです：

( 1  2  3 )
( 4  5  6 )
( 7  8  9 )
(10 11 12 )

ここでは、このFortranのメインテストプログラムt_svd.f90と論理的に同等なPythonコード t_svd.py を作成・実行し、両者の最終的なコンソール出力が完全に一致することを確認しました。

Fortran版の実行結果（抜粋）

 The calculated singular values =    25.4624    1.2907    0.0000    0.0000

      The U-matrix
   -0.1409   -0.8247   -0.1668   -0.5217
   -0.3439   -0.4263    0.6112    0.5713
   -0.5470   -0.0278   -0.7221    0.4225
   -0.7501    0.3706    0.2777   -0.4721

Python版プログラムでも、完全に同一の結果が出力されました。これまでのテストは単一のパターンのみでの検証だったため、より多様なケースでの動作確認を行いました。

より多様な試験での検証

これまでの試験は単一のパターンのみでの検証だったため、より多様な事例での動作確認を行いました。そのために、Alan Miller氏の基本試験を拡張し、12種類の多様な行列パターンと異なるJOBパラメータの組み合わせを含む包括的な試験コード（advanced_tester.py）を作成して検証を行いました。

試験例の詳細:

1. 基本例（4×3行列）: 基本的な長方形行列での動作確認
2. 正方行列・条件数良好（3×3行列）: 数値的に安定した正方行列での試験
   
3. 縦長行列（5×2行列）: 行数が列数より多い行列での動作確認
4. 横長行列（2×5行列）: 列数が行数より多い行列での動作確認
5. ランク落ち行列（3×3行列）: 線形従属な列を持つ行列での特異値ゼロの検出
6. ゼロ行列（3×2行列）: 全要素がゼロの行列での境界条件試験
7. 対角行列（3×3行列）: 対角成分のみを持つ行列での既知の特異値との比較
8. 重複特異値を持つ対角行列（3×3行列）: 同じ特異値が複数存在する事例
9. 最小行列（1×1行列）: 最小サイズでの動作確認
10. 列ベクトル（2×1行列）: 1列のみの行列での試験
11. 行ベクトル（1×2行列）: 1行のみの行列での試験
    
12. 条件数悪化行列（2×2行列）: 数値的に不安定になりやすい行列での収束性確認

さらに、各試験例に対して異なるJOBパラメータ（00: 特異値のみ、01: 特異値+V行列、10: 特異値+完全U行列、21: 特異値+薄いU行列+V行列）での動作も検証しました。

実行結果の例（ランク落ち行列（3×3行列）の部分の出力例）:

--- Test Case 5: Rank Deficient (N=3, P=3, JOB=11) ---
Input Matrix X:
N=3, P=3, JOB=11
Matrix elements (first 5x5 if large):
   1.0000E+00   4.0000E+00   5.0000E+00
   2.0000E+00   5.0000E+00   7.0000E+00
   3.0000E+00   6.0000E+00   9.0000E+00

SVD Results:
INFO = 0
Singular values S =    1.6848E+01   8.1731E-16   0.0000E+00
Expected: One singular value should be close to zero.

これらの全試験例において、Python版とFortran版は数値的にほぼ完全に一致する結果を出力しました。行列サイズは検証の効率性を考慮して比較的小さなもの（最大5×5）に留めましたが、様々な数学的性質（正則性、ランク、条件数）を持つ行列での動作が確認できました。

移植完了後のPythonコード及び検証用コード

この記事で説明した、Fortranから逐次的に移植したPythonコード及び動作検証用コードは、以下よりご参照いただけます。

• Python移植版ソースコード

  • python_src/dsvdc.py: 今回Fortranのロジックを直接的に移植したPythonコードです。

• 動作・性能確認スクリプト

  • t_svd.py: シンプルなテストプログラムt_svd.f90と論理的に同等なPythonコード
  • advanced_tester.py: 12種類の多様な行列パターンでの包括的な動作検証コード
  • benchmark_svd_python_base.py: 性能測定に（以下参照）使用したコード

露呈したパフォーマンスという課題

これまでのテストは主に正しさの検証を目的としていたため小規模なデータセット（最大5×5行列）に限定されていました。そこで、移植したPythonコードがより実用的なサイズでも正常に動作するかを確認するため、800×800要素のランダムな浮動小数点数から成るもう少し大きな正方行列（matrix_800x800_rand_uniform.bin）を用いた動作試験を実施しました。またその際に実行時間も測定してみました。Fortran版・Python版ともに、ディスクからデータを読み込む処理時間は除外し、実際の計算が行われるdsvdc関数の呼び出し部分のみの実行時間を計測しています（FortranではSYSTEM_CLOCKサブルーチン、Pythonではtime.perf_counter()関数を使用して経過時間を計測）。

結果として、Python版も正常に実行完了し、Fortran版と同一の特異値が得られることが確認できました。実行時間については、Fortran版が約1.38秒で処理を完了したのに対し、Python版は約739秒を要し、約536倍の差が生じました。（測定環境：Windows 11 Pro, CPU: Intel Core i7-9750H, gfortran (GCC) 15.1.0 [-O3], Python 3.12.9）

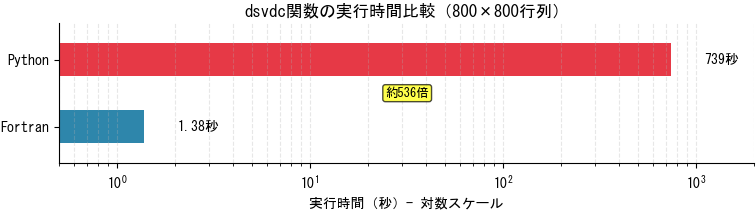
この結果は、インタプリタ言語であるPythonの特性を考慮すれば予想の範囲内ですが、実用的な性能を得るためには追加の最適化が必要であることが確認されました。

次回の第4回「NumPyとNumbaによるPythonコードの高速化」では、プロファイリングによる分析を実施し、「ベクトル化」と「Numbaを用いるJITコンパイル」という2つのアプローチを用いた高速化手法を検証します。また、これらの技術によってPythonコードの性能がどこまで改善されるのかについても見ていきます。