はじめに
要旨
本技術報告書では、ポートフォリオ信用リスクで使用されるモデルの主要な理論的側面を検討します。よく知られているVasicekモデル、大規模同質ポートフォリオ(Vasicek分布)、およびそれらの一般化について紹介します。因子が物流分布に従う例示的なケースを提示します。さまざまな同質ポートフォリオに対する数値実験を行い、これらの手法を比較します。モデルプロトタイプを効率的に実装するために、nAG Toolbox for MATLAB®を使用しています。
序論
信用リスクは銀行業務において重要な分野であり、金融機関、消費者、規制当局など多くの利害関係者に関係します。信用リスクとは、債務者が債務契約上の法的義務を履行できないことから生じる損失のリスクを指します。これをデフォルトイベントと呼びます。
金融機関にとって、ポートフォリオレベルで信用リスクを定量化することが重要です。ポートフォリオの信用損失モデリングには、債務者間のデフォルト依存性を理解する必要があります。一般的なアプローチは、債務者が一部の潜在的な因子(多くの場合、標準正規分布でモデル化される)を条件として独立であると仮定する因子モデルを利用することです。
1. Vasicekモデル
ポートフォリオのデフォルト時間は、複数のリスク因子によって決定されます。ポートフォリオは \(N\) 人の債務者で構成され、各債務者 \(n\) のデフォルトは、その企業の価値の変動によって決定されます。時間 \(t\) における債務者 \(n\) の資産価値を \(V_n(t)\) で表し、企業の価値がデフォルト閾値 \(V_n(T)_n\) を下回った場合、債務者はデフォルトします。
資産価値モデル
債務者の資産価値は、システマティック因子 \(Y\) と特異的因子 \(\epsilon_n\) によって決定されます:
$$ V_n(t) = Y + \epsilon_n $$ここで、\(Y\) と \(\epsilon_n\) は独立で、標準正規分布に従う確率変数です。
条件付きデフォルト確率
システマティック因子 \(Y\) の実現値を条件とするデフォルト確率は以下のように与えられます:
$$ p_n(y) = \Phi(\cdot) $$デフォルト確率関数の計算
デフォルト確率分布を計算するには、特定の積分を評価する必要があります。これはガウス・エルミート求積法を用いて行うことができます。この方法は以下の形式の積分を近似します:
$$ \int_{-\infty}^{\infty} e^{-x^2} f(x) dx \approx \sum_{i=1}^{k} w_i f(x_i) $$ここで、kは求積に使用されるノード数です。
2. 一般化Vasicekモデル
一般化Vasicekモデルでは、分布関数 \(G(y)\) に従う共通因子 \(Y\) と、関数 \(H(\epsilon_n)\) に従って分布する特異的ノイズ成分 \(\epsilon_n\) を導入します。
$$ V_n(t) = Y + \epsilon_n, \quad Y \sim G(y), \quad \epsilon_n \sim H(\epsilon_n) $$一般化されたデフォルト確率は以下のように与えられます:
$$ p_n(y) = H(\cdot) $$ロジスティック因子モデル
一般化Vasicekモデルでは、ロジスティック分布に従う因子を考慮することができます。ロジスティック分布の確率密度関数(PDF)は以下のように与えられます:
$$ f(y; \mu, s) = \frac{e^{-(y-\mu)/s}}{s(1+e^{-(y-\mu)/s})^2} $$累積分布関数(CDF)は以下のようになります:
$$ F(y; \mu, s) = \frac{1}{1+e^{-(y-\mu)/s}} $$モデルを中心化・標準化するために、パラメータ \(\mu = 0\) および \(s = \frac{\sqrt{3}}{\pi}\) を選択し、平均0、分散1を確保します。
3. 大規模ポートフォリオ近似
Vasicek単一因子モデルは、同質な資産を持つ大規模ポートフォリオに有用です。このモデルは、多数の債務者を仮定することで計算を簡略化します。
Vasicek分布
大規模ポートフォリオ近似下でのポートフォリオ損失分布関数は以下のように与えられます:
$$ F(x; p, \rho) = \Phi\left(\frac{\Phi^{-1}(x) - \sqrt{\rho}\Phi^{-1}(p)}{\sqrt{1-\rho}}\right) $$4. 一般損失分布
一般的なポートフォリオ累積分布関数は以下のように与えられます:
$$ F(x; \mu, \sigma) = P(X \leq x) = 1 - G\left(\frac{H^{-1}(x) - \mu}{\sigma}\right) $$対応する確率密度関数は以下のようになります:
$$ f(x; \mu, \sigma) = \frac{1}{\sigma}G'\left(\frac{H^{-1}(x) - \mu}{\sigma}\right) \frac{1}{H'(H^{-1}(x))} $$5. 数値例と分析
表1では、相関(ρ)が増加するにつれて、正確な数値が減少していることがわかります。また、ABS(資産担保証券)とMBS(住宅ローン担保証券)のファクターローディング(w = \(\sqrt{\rho}\))を調整するために使用される標準偏差対平均比という指標も含まれています。
| 相関 (\(\rho\)) | 平均 | 標準偏差 | 標準偏差/平均 | VaR(\(_{0.999}\)) |
|---|---|---|---|---|
| 0.0 | 0.050000 | 0.021794 | 0.4359 | 0.1346 |
| 0.01 | 0.050000 | 0.024119 | 0.4824 | 0.1478 |
| 0.05 | 0.050000 | 0.032215 | 0.6443 | 0.2028 |
| 0.10 | 0.050000 | 0.040935 | 0.8187 | 0.2716 |
| 0.30 | 0.049999 | 0.071157 | 1.4231 | 0.5570 |
| 0.50 | 0.049997 | 0.100325 | 2.0066 | 0.8145 |
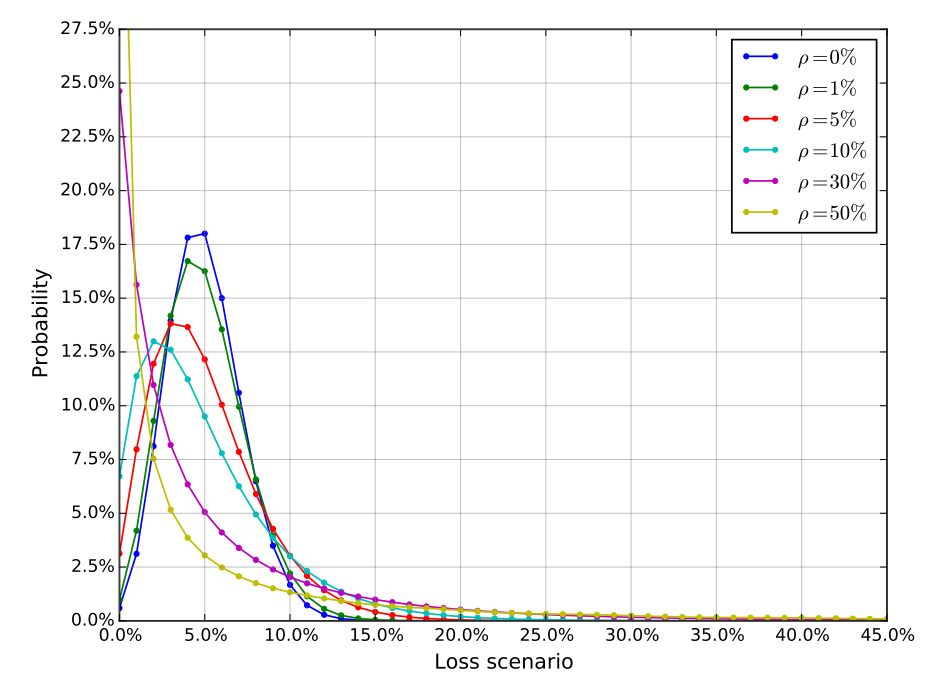
図1: 異なる資産相関下でのデフォルト確率分布。パラメータ: N = 100、p = 5%。資産相関 \(\rho\) はパーセンテージポイントで表示。
6. 結論
本報告書では、ポートフォリオ信用リスクにおけるデフォルト確率の計算に最も広く使用されているモデルについて議論しました。Vasicek単一因子モデルとその非正規因子への一般化を紹介しました。また、大規模ポートフォリオ近似法を提示し、一般損失分布の閉形式表現を生成しました。これらのモデルはnAG Toolbox for MATLABを使用して実装されており、プロトタイピングや異質ポートフォリオへのさらなる拡張に適しています。
7. コード
論文(下記参照※)では、主要なルーチンとしてVasicek単一因子モデル、大規模同質ポートフォリオ、一般化Vasicek単一因子モデル、一般損失分布のためのコードを提供しています。これらのコードは、nAG関数を活用して効率的に実装されています。また、具体的な例として、Vasicekモデルと大規模同質ポートフォリオのロジスティック因子モデルの使用例も示しています。
これらのモデルとコードを使用することで、ポートフォリオ信用リスクの詳細な分析と評価が可能となります。
※この文章は論文の要約であり、論文の本文(英語)、コード等は以下のURLで閲覧できます:
