Keyword: 重回帰分析
概要
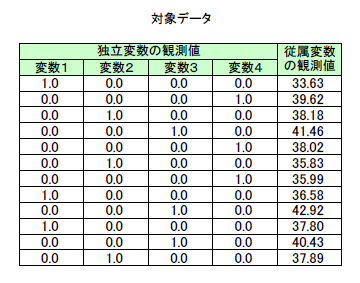
本サンプルは重回帰分析を行うサンプルプログラムです。 本サンプルは以下に示される独立変数の観測値と従属変数の観測値を用いて重回帰分析を行い、独立変数の係数(パラメータ)推定と標準誤差、観測値の残差と対角要素を出力します。
※本サンプルはnAG Toolbox for MATLAB®が提供する関数 g02da() のExampleコードです。実行にはMATLAB®本体(他社製品)とnAG Toolbox for MATLAB®が必要です。
本サンプル及び関数の詳細情報は g02da のマニュアルページをご参照ください。
入力データ
mean = 'M';
weight = 'U';
x = [1, 0, 0, 0;
0, 0, 0, 1;
0, 1, 0, 0;
0, 0, 1, 0;
0, 0, 0, 1;
0, 1, 0, 0;
0, 0, 0, 1;
1, 0, 0, 0;
0, 0, 1, 0;
1, 0, 0, 0;
0, 0, 1, 0;
0, 1, 0, 0];
isx = [int32(1);1;1;1];
ip = int32(5);
y = [33.63;
39.62;
38.18;
41.46;
38.02;
35.83;
35.99;
36.58;
42.92;
37.8;
40.43;
37.89];
wt = [];
[rss, idf, b, se, cov, res, h, q, svd, irank, p, wk, ifail] = g02da(mean, weight, x, isx, ip, y, wt)
- mean には切片が含まれるかどうかを示すパラメータ指定しています。"M"は切片を含むことを意味します。
- weight には重みづけをするかどうかを示すパラメータを指定しています。"W"は重みづけをすることを意味します。
- x には独立変数の観測値を指定しています。
- isx にはどの独立変数がモデルに含まれるかを示すフラグを指定しています。
- ip には独立変数の数を指定しています。
- y には従属変数の観測値を指定しています。
- wt には重みを指定しています。
- 最後に本関数を呼び出す構文を指定しています。
出力結果
rss =
22.2268
idf =
8
b =
30.5567
5.4467
6.7433
11.0467
7.3200
se =
0.3849
0.8390
0.8390
0.8390
0.8390
cov =
0.1482
0.0370
0.7038
0.0370
-0.2223
0.7038
0.0370
-0.2223
-0.2223
0.7038
0.0370
-0.2223
-0.2223
-0.2223
0.7038
res =
-2.3733
1.7433
0.8800
-0.1433
0.1433
-1.4700
-1.8867
0.5767
1.3167
1.7967
-1.1733
0.5900
h =
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
0.3333
q =
-132.3142 -3.4641 -0.8660 -0.8660 -0.8660 -0.8660
-4.3850 0.2543 1.5000 -0.5000 -0.5000 -0.5000
3.4507 0.2543 0.2464 -1.4142 0.7071 0.7071
-4.5642 0.2543 0.2464 -0.1494 -1.2247 1.2247
-0.8332 0.2543 0.2464 -0.1494 -0.2512 0.0000
-2.3000 0.2543 0.2464 0.4236 0.0476 0.5166
-1.8495 0.2543 0.2464 -0.1494 -0.2512 0.1033
1.4560 0.2543 -0.3431 -0.0580 -0.0975 0.3616
1.6828 0.2543 0.2464 -0.1494 0.4137 -0.2066
2.6760 0.2543 -0.3431 -0.0580 -0.0975 0.3616
-0.8072 0.2543 0.2464 -0.1494 0.4137 -0.2066
-0.2400 0.2543 0.2464 0.4236 0.0476 0.5166
svd =
1
irank =
4
p =
1.1352
1.1308
1.2340
1.2280
1.0530
3.8730
1.7321
1.7321
1.7321
0.0000
0.2309
0.0000
0.0000
0.0000
-0.4472
0.0577
-0.4599
0.1809
0.0760
0.4472
0.0577
0.0669
-0.0854
-0.4881
0.4472
0.0577
0.3382
0.3322
0.1590
0.4472
0.0577
0.0548
-0.4277
0.2531
0.4472
wk =
-1.0000
0.0000
-0.0000
0.0000
0.0000
-0.0000
-0.9198
0.1832
-0.3470
0.0000
-0.0000
0.3618
0.0533
-0.9307
-0.0000
-0.0000
0.1521
0.9816
0.1153
0.0000
0.0000
0.0000
-0.0000
-0.0000
1.0000
0.2887
0.0669
-0.0854
-0.4881
4.0000
3.2500
4.2500
5.2500
5.2500
-0.0000
0.6239
0.8215
0.9995
1.0000
0.7815
0.5702
0.0312
0.0000
-0.6239
-0.8215
ifail =
0
- rss は回帰モデルの残差平方和を示しています。
- idf は残差平方和に関連する自由度を示しています。
- b の6行目は回帰モデルの切片の推定値を示し、7〜10行目は独立変数の係数を示しています。
- se は上記のパラメータ推定の標準誤差を示しています。
- cov はパラメータ推定の分散共分散行列の上三角部分を示しています。
- res は重みづけされた残差を示しています。
- h は三重対角要素を示しています。
- q は QR 分解の結果を示しています。
- svd は特異値分解が行われたかどうかを示しています。"1"は行われたことを意味します。
- irank は独立変数のランクを示しています。
- p は QR 分解と特異値分解の詳細を示しています。
- wk は特異値分解の場合に、一般線形回帰のパラメータ推定値を計算する関数 g02dg で必要とされる情報を示しています。
- ifail は関数がエラーを検知しなければ"0"が出力されます。
