Keyword: 主成分分析, 多変量解析
概要
本サンプルは主成分分析を行うサンプルプログラムです。 本サンプルは以下の「分析対象データ」に示される変数が3個で観察数が10のデータを分析対象とします。 このサンプルでは主成分分析を行い、固有値、寄与度、χ二乗値、自由度、有意度、主成分負荷量、主成分スコアを出力します。
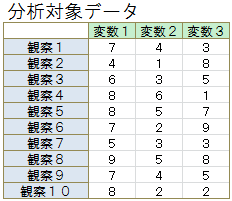
※本サンプルはnAG Toolbox for MATLAB®が提供する関数 g03aa() のExampleコードです。実行にはMATLAB®本体(他社製品)とnAG Toolbox for MATLAB®が必要です。
本サンプル及び関数の詳細情報は g03aa のマニュアルページをご参照ください。
入力データ
matrix = 'V';
std = 'E';
weight = 'U';
x = [7, 4, 3;
4, 1, 8;
6, 3, 5;
8, 6, 1;
8, 5, 7;
7, 2, 9;
5, 3, 3;
9, 5, 8;
7, 4, 5;
8, 2, 2];
isx = [int32(1);1;1];
s = [-5.04677090184712e-39;
-5.04512289241806e-39;
-1.790699005126953];
wt = [0];
nvar = int32(3);
[sOut, e, p, v, ifail] = g03aa(matrix, std, weight, x, isx, s, wt, nvar)
- matrix には計算の際に用いる行列の種類を指定しています。"V"は分散共分散行列を用いることを意味します。
- std には計算に利用する主成分スコアのタイプを指定しています。"E"は主成分スコアに(分散が対応する固有値と同じになるように)標準化されたものを使う事を意味しています。
- weight には重み付けをするかどうかを指定しています。"U"は重みを付けない事を意味しています。
- x には観察データを与えています。各行はそれぞれの観察値であり、3つの値を持っています。
- isx には計算で使う変数がどれであるかを指定しています。ここで 1 は計算で使う事を示しています。(0は計算で当該変数を使わないことを示します。ここで与える数字は変数の数分(ここでは3)なければなりません。 今回のデータはすべての変数を計算で使うので3つの 1 が与えられています。
- s には標準化係数を与えています。
- wt には重み付けをする場合はその重みを指定します。この場合は重み付けをしないのでこの値は参照されません。
- nvar には出力として得たい主成分の数(=3)を指定しています。この数値は変数の数を超えてはいけません。
- 最後に本関数を呼び出す構文が指定されています。
出力結果
sOut =
-0.0000
-0.0000
-1.7907
e =
8.2739 0.6515 0.6515 8.6127 5.0000 0.1255
3.6761 0.2895 0.9410 4.1183 2.0000 0.1276
0.7499 0.0590 1.0000 0 0 0
p =
-0.1376 0.6990 -0.7017
-0.2505 0.6609 0.7075
0.9583 0.2731 0.0842
v =
-2.1514 -0.1731 0.1068
3.8042 -2.8875 0.5104
0.1532 -0.9869 0.2694
-4.7065 1.3015 0.6517
1.2938 2.2791 0.4492
4.0993 0.1436 -0.8031
-1.6258 -2.2321 0.8028
2.1145 3.2512 -0.1684
-0.2348 0.3730 0.2751
-2.7464 -1.0689 -2.0940
ifail =
0
- sOut は入力データの標準化係数をそのまま出力しています。
- e は各主成分の固有値 、寄与度 、累積寄与度、χ二乗値 、自由度、有意度 を示しています。各行は上から順番に第一主成分、第二主成分、第三主成分の各値を示しています。
- p は主成分負荷量を示しています。
- v は主成分スコアを示しています。 行方向は観察データ、列方向は主成分をそれぞれ表しています。
- ifail は関数がエラーを検知しなければ"0"が出力されます。
リファレンス
サンプル入力データは Cooley W C and Lohnes P R (1971) Multivariate Data Analysis Wiley よりのデータです。
