Keyword: 複素多項式の根
概要
本サンプルは複素多項式の根を求めるFortranによるサンプルプログラムです。 本サンプルは一つ目の例では以下に示される次数が5の複素多項式の根を求めて出力します。二つめの例では同じ問題を解き求められた解の誤差推定を出力します。
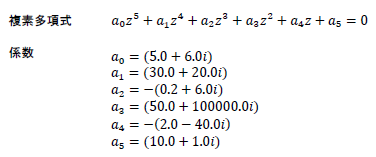
※本サンプルはnAG Fortranライブラリに含まれるルーチン c02aff() のExampleコードです。本サンプル及びルーチンの詳細情報は c02aff のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はc02aff のマニュアルページを参照)| このデータをダウンロード |
C02AFF Example Program Data
Example 1
5
5.0 6.0
30.0 20.0
-0.2 -6.0
50.0 100000.0
-2.0 40.0
10.0 1.0
Example 2
5
5.0 6.0
30.0 20.0
-0.2 -6.0
50.0 100000.0
-2.0 40.0
10.0 1.0
- 1行目はタイトル行で読み飛ばされます。
- 4行目に一つ目の例の多項式の次数(n)を指定しています。
- 5〜10行目に一つ目の例の各項の係数の実部と虚部(a)を指定しています。
- 13行目に二つ目の例の多項式の次数(n)を指定しています。
- 14〜19行目に二つ目の例の各項の係数の実部と虚部(a)を指定しています。
出力結果
(本ルーチンの詳細はc02aff のマニュアルページを参照)| この出力例をダウンロード |
C02AFF Example Program Results
Example 1
Degree of polynomial = 5
Computed roots of polynomial
z = -2.4328E+01 -4.8555E+00*i
z = 5.2487E+00 +2.2736E+01*i
z = 1.4653E+01 -1.6569E+01*i
z = -6.9264E-03 -7.4434E-03*i
z = 6.5264E-03 +7.4232E-03*i
Example 2
Degree of polynomial = 5
Computed roots of polynomial Error estimates
(machine-dependent)
z = -2.4328E+01 -4.8555E+00*i 1.4E-16
z = 5.2487E+00 +2.2736E+01*i 3.0E-16
z = 1.4653E+01 -1.6569E+01*i 4.8E-16
z = -6.9264E-03 -7.4434E-03*i 1.7E-16
z = 6.5264E-03 +7.4232E-03*i 1.1E-16
- 5行目に一つ目の例の入力された多項式の次数が出力されています。
- 9〜13行目に一つ目の例の複素多項式の根(実部と虚部)が出力されています。
- 18行目に二つ目の例の入力された多項式の次数が出力されています。
- 23〜27行目に二つ目の例の複素多項式の根(実部と虚部)と誤差推定が出力されています。
ソースコード
(本ルーチンの詳細はc02aff のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
! C02AFF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
MODULE c02affe_mod
! C02AFF Example Program Module: Parameters
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
LOGICAL, PARAMETER :: scal = .TRUE.
END MODULE c02affe_mod
PROGRAM c02affe
! C02AFF Example Main Program
! .. Use Statements ..
USE c02affe_mod, ONLY : nout
! .. Implicit None Statement ..
IMPLICIT NONE
! .. External Subroutines ..
EXTERNAL ex1, ex2
! .. Executable Statements ..
WRITE (nout,*) 'C02AFF Example Program Results'
CALL ex1
CALL ex2
END PROGRAM c02affe
SUBROUTINE ex1
! .. Use Statements ..
USE nag_library, ONLY : c02aff, nag_wp
USE c02affe_mod, ONLY : nin, nout, scal
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
INTEGER :: i, ifail, n
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), w(:), z(:,:)
! .. Executable Statements ..
WRITE (nout,*)
WRITE (nout,*)
WRITE (nout,*) 'Example 1'
! Skip heading in data file
READ (nin,*)
READ (nin,*)
READ (nin,*)
READ (nin,*) n
ALLOCATE (a(2,0:n),w(4*(n+1)),z(2,n))
READ (nin,*) (a(1,i),a(2,i),i=0,n)
ifail = 0
CALL c02aff(a,n,scal,z,w,ifail)
WRITE (nout,*)
WRITE (nout,99999) 'Degree of polynomial = ', n
WRITE (nout,*)
WRITE (nout,*) 'Computed roots of polynomial'
WRITE (nout,*)
DO i = 1, n
WRITE (nout,99998) 'z = ', z(1,i), z(2,i), '*i'
END DO
99999 FORMAT (1X,A,I4)
99998 FORMAT (1X,A,1P,E12.4,SP,E12.4,A)
END SUBROUTINE ex1
SUBROUTINE ex2
! .. Use Statements ..
USE nag_library, ONLY : a02abf, c02aff, nag_wp, x02ajf, x02alf
USE c02affe_mod, ONLY : nin, nout, scal
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
REAL (KIND=nag_wp) :: deltac, deltai, di, eps, epsbar, f, &
r1, r2, r3, rmax
INTEGER :: i, ifail, j, jmin, n
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), abar(:,:), r(:), w(:), &
z(:,:), zbar(:,:)
INTEGER, ALLOCATABLE :: m(:)
! .. Intrinsic Functions ..
INTRINSIC abs, max, min
! .. Executable Statements ..
WRITE (nout,*)
WRITE (nout,*)
WRITE (nout,*) 'Example 2'
! Skip heading in data file
READ (nin,*)
READ (nin,*)
READ (nin,*) n
ALLOCATE (a(2,0:n),abar(2,0:n),r(n),w(4*(n+1)),z(2,n),zbar(2,n),m(n))
! Read in the coefficients of the original polynomial.
READ (nin,*) (a(1,i),a(2,i),i=0,n)
! Compute the roots of the original polynomial.
ifail = 0
CALL c02aff(a,n,scal,z,w,ifail)
! Form the coefficients of the perturbed polynomial.
eps = x02ajf()
epsbar = 3.0E0_nag_wp*eps
DO i = 0, n
IF (a(1,i)/=0.0E0_nag_wp) THEN
f = 1.0E0_nag_wp + epsbar
epsbar = -epsbar
abar(1,i) = f*a(1,i)
IF (a(2,i)/=0.0E0_nag_wp) THEN
abar(2,i) = f*a(2,i)
ELSE
abar(2,i) = 0.0E0_nag_wp
END IF
ELSE
abar(1,i) = 0.0E0_nag_wp
IF (a(2,i)/=0.0E0_nag_wp) THEN
f = 1.0E0_nag_wp + epsbar
epsbar = -epsbar
abar(2,i) = f*a(2,i)
ELSE
abar(2,i) = 0.0E0_nag_wp
END IF
END IF
END DO
! Compute the roots of the perturbed polynomial.
ifail = 0
CALL c02aff(abar,n,scal,zbar,w,ifail)
! Perform error analysis.
! Initialize markers to 0 (unmarked).
m(1:n) = 0
rmax = x02alf()
! Loop over all unperturbed roots (stored in Z).
DO i = 1, n
deltai = rmax
r1 = a02abf(z(1,i),z(2,i))
! Loop over all perturbed roots (stored in ZBAR).
DO j = 1, n
! Compare the current unperturbed root to all unmarked
! perturbed roots.
IF (m(j)==0) THEN
r2 = a02abf(zbar(1,j),zbar(2,j))
deltac = abs(r1-r2)
IF (deltac<deltai) THEN
deltai = deltac
jmin = j
END IF
END IF
END DO
! Mark the selected perturbed root.
m(jmin) = 1
! Compute the relative error.
IF (r1/=0.0E0_nag_wp) THEN
r3 = a02abf(zbar(1,jmin),zbar(2,jmin))
di = min(r1,r3)
r(i) = max(deltai/max(di,deltai/rmax),eps)
ELSE
r(i) = 0.0E0_nag_wp
END IF
END DO
WRITE (nout,*)
WRITE (nout,99999) 'Degree of polynomial = ', n
WRITE (nout,*)
WRITE (nout,*) 'Computed roots of polynomial ', ' Error estimates'
WRITE (nout,*) ' ', ' (machine-dependent)'
WRITE (nout,*)
DO i = 1, n
WRITE (nout,99998) 'z = ', z(1,i), z(2,i), '*i', r(i)
END DO
99999 FORMAT (1X,A,I4)
99998 FORMAT (1X,A,1P,E12.4,SP,E12.4,A,5X,SS,E9.1)
END SUBROUTINE ex2
