Keyword: 実スパース, 連立方程式, 誤差限界, 解の改良
概要
本サンプルは実スパース連立方程式の誤差限界をもつ解の改良を行うFortranによるサンプルプログラムです。 本サンプルは以下に示される実スパース連立方程式を反復改良を用いて解き、解と前進誤差と後退誤差を出力します。
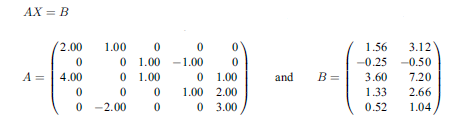
※本サンプルはnAG Fortranライブラリに含まれるルーチン f11mhf() のExampleコードです。本サンプル及びルーチンの詳細情報は f11mhf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はf11mhf のマニュアルページを参照)| このデータをダウンロード |
F11MHF Example Program Data 5 2 N, NRHS 1 3 5 7 9 12 ICOLZP(I) I=1,..,N+1 2. 1 4. 3 1. 1 -2. 5 1. 2 1. 3 -1. 2 1. 4 1. 3 2. 4 3. 5 A(I), IROWIX(I) I=1,NNZ 1.56 -.25 3.6 1.33 .52 3.12 -.50 7.2 2.66 1.04 X(I,J) J=1,NRHS I=1,N
- 1行目はタイトル行で読み飛ばされます。
- 2行目に行列Aの次数(n)とBの右辺の数(nrhs)を指定しています。
- 3〜8行目に行列Aの列の先頭の非ゼロ要素のインデックス(icolzp)を指定しています。
- 9〜19行目に行列Aの非ゼロ値とその行インデックス(irowix)を指定しています。
- 20〜21行目に解の行列Xの要素の値(x)を指定しています。
出力結果
(本ルーチンの詳細はf11mhf のマニュアルページを参照)| この出力例をダウンロード |
F11MHF Example Program Results
Solutions
1 2
1 0.7000 1.4000
2 0.1600 0.3200
3 0.5200 1.0400
4 0.7700 1.5400
5 0.2800 0.5600
Estimated Forward Error
5.0E-15
5.0E-15
Backward Error
3.6E-17
3.6E-17
- 5〜9行目に改良された解が出力されています。
- 11〜12行目に前進誤差限界の推定値が出力されています。
- 14〜15行目に後退誤差限界が出力されています。
ソースコード
(本ルーチンの詳細はf11mhf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM f11mhfe
! F11MHF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : f11mdf, f11mef, f11mff, f11mhf, nag_wp, x04caf, &
x04cbf
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
REAL (KIND=nag_wp), PARAMETER :: one = 1.E0_nag_wp
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: flop, thresh
INTEGER :: i, ifail, j, ldb, ldx, n, nnz, nnzl, &
nnzu, nrhs, nzlmx, nzlumx, nzumx
CHARACTER (1) :: spec, trans
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:), b(:,:), berr(:), ferr(:), &
lval(:), uval(:), x(:,:)
INTEGER, ALLOCATABLE :: icolzp(:), il(:), iprm(:), &
irowix(:), iu(:)
CHARACTER (1) :: clabs(1), rlabs(1)
! .. Executable Statements ..
WRITE (nout,*) 'F11MHF Example Program Results'
FLUSH (nout)
! Skip heading in data file
READ (nin,*)
! Read order of matrix and number of right hand sides
READ (nin,*) n, nrhs
ldb = n
ldx = n
ALLOCATE (b(ldb,nrhs),berr(nrhs),ferr(nrhs),x(ldx,nrhs),icolzp(n+1), &
iprm(7*n))
! Read the matrix A
READ (nin,*) icolzp(1:n+1)
nnz = icolzp(n+1) - 1
ALLOCATE (a(nnz),lval(8*nnz),uval(8*nnz),il(7*n+8*nnz+4),irowix(nnz), &
iu(2*n+8*nnz+1))
DO i = 1, nnz
READ (nin,*) a(i), irowix(i)
END DO
! Read the right hand sides
DO j = 1, nrhs
READ (nin,*) x(1:n,j)
b(1:n,j) = x(1:n,j)
END DO
! Calculate COLAMD permutation
spec = 'M'
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
CALL f11mdf(spec,n,icolzp,irowix,iprm,ifail)
! Factorise
thresh = one
ifail = 0
nzlmx = 8*nnz
nzlumx = 8*nnz
nzumx = 8*nnz
CALL f11mef(n,irowix,a,iprm,thresh,nzlmx,nzlumx,nzumx,il,lval,iu,uval, &
nnzl,nnzu,flop,ifail)
! Compute solution in array X
trans = 'N'
ifail = 0
CALL f11mff(trans,n,iprm,il,lval,iu,uval,nrhs,x,ldx,ifail)
! Improve solution, and compute backward errors and estimated
! bounds on the forward errors
CALL f11mhf(trans,n,icolzp,irowix,a,iprm,il,lval,iu,uval,nrhs,b,ldb,x, &
ldx,ferr,berr,ifail)
! Print solution
WRITE (nout,*)
FLUSH (nout)
CALL x04caf('G',' ',n,nrhs,x,ldx,'Solutions',ifail)
CALL x04cbf('G','X',nrhs,1,ferr,nrhs,'1PE8.1', &
'Estimated Forward Error','N',rlabs,'N',clabs,80,0,ifail)
CALL x04cbf('G','X',nrhs,1,berr,nrhs,'1PE8.1','Backward Error','N', &
rlabs,'N',clabs,80,0,ifail)
END PROGRAM f11mhfe
