Keyword: 共役勾配, ランチョス, Lanczos, スパース, 対称, 線形連立方程式
概要
本サンプルは共役勾配/ランチョス(Lanczos)法を用いて実スパース対称線形連立方程式を解くFortranによるサンプルプログラムです。 本サンプルは共役勾配を用いて以下に示される対称線形連立方程式を解いて解を出力します。
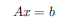
※本サンプルはnAG Fortranライブラリに含まれるルーチン f11jcf() のExampleコードです。本サンプル及びルーチンの詳細情報は f11jcf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はf11jcf のマニュアルページを参照)| このデータをダウンロード |
F11JCF Example Program Data 7 N 16 NNZ 'CG' METHOD 1 0.0 LFILL, DTOL 'N' 0.0 MIC, DSCALE 'M' PSTRAT 1.0D-6 100 TOL, MAXITN 4. 1 1 1. 2 1 5. 2 2 2. 3 3 2. 4 2 3. 4 4 -1. 5 1 1. 5 4 4. 5 5 1. 6 2 -2. 6 5 3. 6 6 2. 7 1 -1. 7 2 -2. 7 3 5. 7 7 A(I), IROW(I), ICOL(I), I=1,...,NNZ 15. 18. -8. 21. 11. 10. 29. B(I), I=1,...,N 0. 0. 0. 0. 0. 0. 0. X(I), I=1,...,N
- 1行目はタイトル行で読み飛ばされます。
- 2行目に行列Aの次数(n=7)を指定しています。
- 3行目に行列Aの下三角部分の非ゼロ要素の数(nnz=16)を指定しています。
- 4行目に反復手法(method='CG':共役勾配法(Conjugate Gradient method))を指定しています。
- 5行目の1番目のパラメータ(lfill)は値が0以上の場合、分解で許されたフィル(fill)の最大レベルを指定しています。2番目のパラメータ(dtol)は、1番目のパラメータの値が負の値の場合、フィルイン(fill-in)を制御するためのドロップ許容値を指定しています。1番目のパラメータの値が0以上の場合は2番目のパラメータの値は参照されません。
- 6行目には行の合計を保持するためにコレスキー分解が修正されるかどうか(mic='N':修正されない)と対角スケーリング引数(dscale=0.0)を指定しています。
- 7行目にピボット法(pstrat='M':Markowitz法を用いて対角ピボットが実行される)を指定しています。
- 8行目に許容値(tol=1.0D-6)と最大反復数(maxitn=100)を指定しています。
- 9〜24行目に行列Aの非ゼロ要素(a)、行列Aの非ゼロ要素の行インデックス(irow)、列インデックス(icol)を指定しています。
- 25〜26行目に右辺ベクトルBを指定しています。
- 27〜28行目に解ベクトルxの初期近似値を指定しています。
出力結果
(本ルーチンの詳細はf11jcf のマニュアルページを参照)| この出力例をダウンロード |
F11JCF Example Program Results
Converged in 1 iterations
Final residual norm = 7.105E-15
1.0000E+00
2.0000E+00
3.0000E+00
4.0000E+00
5.0000E+00
6.0000E+00
7.0000E+00
- 2行目には1回の反復で収束したことが示されています。
- 3行目に最終的な残差ノルムが出力されています。
- 4〜10行目に解ベクトルxの改良された近似値が出力されています。
ソースコード
(本ルーチンの詳細はf11jcf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM f11jcfe
! F11JCF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : f11jaf, f11jcf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: dscale, dtol, rnorm, tol
INTEGER :: i, ifail, itn, la, lfill, liwork, &
lwork, maxitn, n, nnz, nnzc, npivm
CHARACTER (6) :: method
CHARACTER (1) :: mic, pstrat
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:), b(:), work(:), x(:)
INTEGER, ALLOCATABLE :: icol(:), ipiv(:), irow(:), istr(:), &
iwork(:)
! .. Executable Statements ..
WRITE (nout,*) 'F11JCF Example Program Results'
! Skip heading in data file
READ (nin,*)
! Read algorithmic parameters
READ (nin,*) n
READ (nin,*) nnz
la = 3*nnz
liwork = 2*la + 7*n + 1
lwork = 6*n + 120
ALLOCATE (a(la),b(n),work(lwork),x(n),icol(la),ipiv(n),irow(la), &
istr(n+1),iwork(liwork))
READ (nin,*) method
READ (nin,*) lfill, dtol
READ (nin,*) mic, dscale
READ (nin,*) pstrat
READ (nin,*) tol, maxitn
! Read the matrix A
DO i = 1, nnz
READ (nin,*) a(i), irow(i), icol(i)
END DO
! Read right-hand side vector b and initial approximate solution x
READ (nin,*) b(1:n)
READ (nin,*) x(1:n)
! Calculate incomplete Cholesky factorization
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
CALL f11jaf(n,nnz,a,la,irow,icol,lfill,dtol,mic,dscale,pstrat,ipiv, &
istr,nnzc,npivm,iwork,liwork,ifail)
! Solve Ax = b using F11JCF
ifail = 0
CALL f11jcf(method,n,nnz,a,la,irow,icol,ipiv,istr,b,tol,maxitn,x,rnorm, &
itn,work,lwork,ifail)
WRITE (nout,99999) 'Converged in', itn, ' iterations'
WRITE (nout,99998) 'Final residual norm =', rnorm
! Output x
WRITE (nout,99997) x(1:n)
99999 FORMAT (1X,A,I10,A)
99998 FORMAT (1X,A,1P,E16.3)
99997 FORMAT (1X,1P,E16.4)
END PROGRAM f11jcfe
