Keyword: 数値解析, ブラック・ショールズ, Black-Scholes
概要
本サンプルは数値解析によりブラック・ショールズ(Black-Scholes)方程式を解くFortranによるサンプルプログラムです。 本サンプルは行使価格50ドル、無リスク金利10%、ボラティリティ40%、無配当の5か月満期のアメリカンコールオプションについて以下に示されるブラック・ショールズ(Black-Scholes)方程式を解いてオプション価格とグリークス(Delta, Gamma, Lambda, Theta, Rho)を出力します。
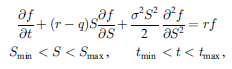
※本サンプルはnAG Fortranライブラリに含まれるルーチン d03ndf() のExampleコードです。本サンプル及びルーチンの詳細情報は d03ndf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はd03ndf のマニュアルページを参照)| このデータをダウンロード |
D03NDF Example Program Data 21 4 : ns, nt 2 : kopt 50. : x 0.4166667 : tmat 0.0 0.1 0.4 : q(1), r(1), sigma(1) 0.0 100. : s(1), s(ns) 0.0 0.125 : t(1), t(nt) .FALSE. .FALSE. .FALSE. : tdpar
- 1行目はタイトル行で読み飛ばされます。
- 2行目に株価の数(ns=21)、タイムステップの数(nt=4)を指定しています。
- 3行目にオプションの種類(kopt=2:アメリカンコールオプション)を指定しています。
- 4行目に行使価格(x=50.)を指定しています。
- 5行目にオプションの満期(tmat=0.4166667)を指定しています。
- 6行目に連続配当 q の定値(q(1)=0.0)、無リスク金利 r の定値(r(1)=0.1)、ボラティリティ σ の定値(sigma(1)=0.4)を指定しています。
- 7行目にオプション価格とグリークスが計算される株価の最小価格(s(1)=0.0)と最大価格(s(21)=100.)を指定しています。
- 8行目にオプション価格とグリークスが計算される期間の最小値(t(1)=0.0)と最大値(t(4)=0.125)を指定しています。
- 9行目にパラメータ r が時間依存かどうか(tdpar(1)=.FALSE.:一定)、パラメータ q が時間依存かどうか(tdpar(2)=.FALSE.:一定)、パラメータ σが時間依存かどうか(tdpar(3)=.FALSE.:一定)を指定しています。
出力結果
(本ルーチンの詳細はd03ndf のマニュアルページを参照)| この出力例をダウンロード |
D03NDF Example Program Results
Option Values
-------------
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | 4.4491E-19 4.5989E-21 1.5461E-23 1.0478E-26
1.0000E+01 | 5.5566E-10 5.5129E-11 3.1298E-12 8.0281E-14
1.5000E+01 | 4.7337E-06 1.2187E-06 2.2774E-07 2.7003E-08
2.0000E+01 | 7.2236E-04 3.1054E-04 1.1005E-04 2.9678E-05
2.5000E+01 | 1.6557E-02 9.6610E-03 5.0099E-03 2.2012E-03
3.0000E+01 | 1.3307E-01 9.4037E-02 6.1869E-02 3.6848E-02
3.5000E+01 | 5.6631E-01 4.5257E-01 3.4667E-01 2.5053E-01
4.0000E+01 | 1.6004E+00 1.3850E+00 1.1699E+00 9.5640E-01
4.5000E+01 | 3.4384E+00 3.1328E+00 2.8168E+00 2.4891E+00
5.0000E+01 | 6.1165E+00 5.7600E+00 5.3874E+00 4.9960E+00
5.5000E+01 | 9.5300E+00 9.1645E+00 8.7846E+00 8.3882E+00
6.0000E+01 | 1.3509E+01 1.3163E+01 1.2808E+01 1.2445E+01
6.5000E+01 | 1.7883E+01 1.7568E+01 1.7251E+01 1.6932E+01
7.0000E+01 | 2.2513E+01 2.2230E+01 2.1949E+01 2.1671E+01
7.5000E+01 | 2.7301E+01 2.7045E+01 2.6792E+01 2.6544E+01
8.0000E+01 | 3.2182E+01 3.1946E+01 3.1713E+01 3.1485E+01
8.5000E+01 | 3.7117E+01 3.6894E+01 3.6674E+01 3.6458E+01
9.0000E+01 | 4.2081E+01 4.1868E+01 4.1656E+01 4.1446E+01
9.5000E+01 | 4.7062E+01 4.6854E+01 4.6647E+01 4.6441E+01
1.0000E+02 | 5.2052E+01 5.1847E+01 5.1643E+01 5.1439E+01
Theta
-----
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | -4.4017E-17 -5.5977E-19 -2.3735E-21 -2.0936E-24
1.0000E+01 | -2.7827E-08 -3.3857E-09 -2.4163E-10 -8.0398E-12
1.5000E+01 | -1.3953E-04 -4.3864E-05 -1.0258E-05 -1.5706E-06
2.0000E+01 | -1.3287E-02 -6.9342E-03 -3.0567E-03 -1.0576E-03
2.5000E+01 | -1.9512E-01 -1.3714E-01 -8.7730E-02 -4.9018E-02
3.0000E+01 | -1.0161E+00 -8.5596E-01 -6.8695E-01 -5.1395E-01
3.5000E+01 | -2.8112E+00 -2.6426E+00 -2.4328E+00 -2.1723E+00
4.0000E+01 | -5.1662E+00 -5.1709E+00 -5.1500E+00 -5.0892E+00
4.5000E+01 | -7.2196E+00 -7.4540E+00 -7.7180E+00 -8.0183E+00
5.0000E+01 | -8.3848E+00 -8.7388E+00 -9.1543E+00 -9.6525E+00
5.5000E+01 | -8.6152E+00 -8.9372E+00 -9.3056E+00 -9.7329E+00
6.0000E+01 | -8.2058E+00 -8.4077E+00 -8.6186E+00 -8.8343E+00
6.5000E+01 | -7.5116E+00 -7.5845E+00 -7.6368E+00 -7.6553E+00
7.0000E+01 | -6.7905E+00 -6.7711E+00 -6.7202E+00 -6.6262E+00
7.5000E+01 | -6.1758E+00 -6.1099E+00 -6.0160E+00 -5.8893E+00
8.0000E+01 | -5.7084E+00 -5.6310E+00 -5.5359E+00 -5.4234E+00
8.5000E+01 | -5.3786E+00 -5.3103E+00 -5.2340E+00 -5.1533E+00
9.0000E+01 | -5.1582E+00 -5.1071E+00 -5.0551E+00 -5.0062E+00
9.5000E+01 | -5.0165E+00 -4.9835E+00 -4.9536E+00 -4.9298E+00
1.0000E+02 | -4.9281E+00 -4.9107E+00 -4.8979E+00 -4.8916E+00
Delta
-----
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | 3.1381E-18 3.5969E-20 1.3576E-22 1.0494E-25
1.0000E+01 | 1.4005E-09 1.5376E-10 9.7805E-12 2.8553E-13
1.5000E+01 | 6.1418E-06 1.7452E-06 3.6436E-07 4.9030E-08
2.0000E+01 | 5.6040E-04 2.6494E-04 1.0451E-04 3.1863E-05
2.5000E+01 | 8.3312E-03 5.3217E-03 3.0570E-03 1.5104E-03
3.0000E+01 | 4.5711E-02 3.5158E-02 2.5461E-02 1.6934E-02
3.5000E+01 | 1.3765E-01 1.1889E-01 9.9459E-02 7.9557E-02
4.0000E+01 | 2.8307E-01 2.6258E-01 2.3996E-01 2.1479E-01
4.5000E+01 | 4.5320E-01 4.3858E-01 4.2214E-01 4.0335E-01
5.0000E+01 | 6.1427E-01 6.0856E-01 6.0249E-01 5.9601E-01
5.5000E+01 | 7.4525E-01 7.4687E-01 7.4937E-01 7.5308E-01
6.0000E+01 | 8.4052E-01 8.4611E-01 8.5298E-01 8.6148E-01
6.5000E+01 | 9.0433E-01 9.1096E-01 9.1862E-01 9.2752E-01
7.0000E+01 | 9.4449E-01 9.5045E-01 9.5699E-01 9.6412E-01
7.5000E+01 | 9.6862E-01 9.7325E-01 9.7808E-01 9.8300E-01
8.0000E+01 | 9.8260E-01 9.8589E-01 9.8913E-01 9.9221E-01
8.5000E+01 | 9.9050E-01 9.9269E-01 9.9473E-01 9.9653E-01
9.0000E+01 | 9.9487E-01 9.9627E-01 9.9748E-01 9.9848E-01
9.5000E+01 | 9.9725E-01 9.9811E-01 9.9881E-01 9.9935E-01
1.0000E+02 | 9.9854E-01 9.9905E-01 9.9945E-01 9.9972E-01
Gamma
-----
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | 2.1246E-17 2.7112E-19 1.1536E-21 1.0211E-24
1.0000E+01 | 3.3102E-09 4.0468E-10 2.9020E-11 9.7029E-13
1.5000E+01 | 7.2660E-06 2.2982E-06 5.4080E-07 8.3319E-08
2.0000E+01 | 3.8245E-04 2.0111E-04 8.9333E-05 3.1153E-05
2.5000E+01 | 3.5190E-03 2.4960E-03 1.6118E-03 9.0924E-04
3.0000E+01 | 1.2392E-02 1.0554E-02 8.5660E-03 6.4838E-03
3.5000E+01 | 2.4348E-02 2.3181E-02 2.1626E-02 1.9580E-02
4.0000E+01 | 3.2765E-02 3.3274E-02 3.3650E-02 3.3795E-02
4.5000E+01 | 3.4099E-02 3.5763E-02 3.7655E-02 3.9828E-02
5.0000E+01 | 2.9625E-02 3.1360E-02 3.3403E-02 3.5860E-02
5.5000E+01 | 2.2600E-02 2.3743E-02 2.5052E-02 2.6569E-02
6.0000E+01 | 1.5672E-02 1.6137E-02 1.6603E-02 1.7048E-02
6.5000E+01 | 1.0123E-02 1.0119E-02 1.0032E-02 9.8216E-03
7.0000E+01 | 6.1999E-03 5.9720E-03 5.6534E-03 5.2154E-03
7.5000E+01 | 3.6474E-03 3.3666E-03 3.0215E-03 2.6027E-03
8.0000E+01 | 2.0815E-03 1.8329E-03 1.5510E-03 1.2387E-03
8.5000E+01 | 1.1610E-03 9.7196E-04 7.7211E-04 5.6851E-04
9.0000E+01 | 6.3660E-04 5.0529E-04 3.7553E-04 2.5382E-04
9.5000E+01 | 3.4468E-04 2.5884E-04 1.7950E-04 1.1099E-04
1.0000E+02 | 1.8494E-04 1.3118E-04 8.4708E-05 4.7786E-05
Lambda
------
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | 8.8525E-17 1.0167E-18 3.8453E-21 2.9781E-24
1.0000E+01 | 5.5171E-08 6.0702E-09 3.8694E-10 1.1320E-11
1.5000E+01 | 2.7247E-04 7.7565E-05 1.6224E-05 2.1871E-06
2.0000E+01 | 2.5496E-02 1.2066E-02 4.7644E-03 1.4538E-03
2.5000E+01 | 3.6656E-01 2.3400E-01 1.3431E-01 6.6299E-02
3.0000E+01 | 1.8588E+00 1.4248E+00 1.0279E+00 6.8080E-01
3.5000E+01 | 4.9710E+00 4.2595E+00 3.5323E+00 2.7983E+00
4.0000E+01 | 8.7374E+00 7.9857E+00 7.1787E+00 6.3084E+00
4.5000E+01 | 1.1508E+01 1.0863E+01 1.0167E+01 9.4094E+00
5.0000E+01 | 1.2344E+01 1.1760E+01 1.1134E+01 1.0459E+01
5.5000E+01 | 1.1394E+01 1.0773E+01 1.0104E+01 9.3768E+00
6.0000E+01 | 9.4033E+00 8.7137E+00 7.9693E+00 7.1602E+00
6.5000E+01 | 7.1285E+00 6.4127E+00 5.6514E+00 4.8412E+00
7.0000E+01 | 5.0632E+00 4.3894E+00 3.6936E+00 2.9815E+00
7.5000E+01 | 3.4194E+00 2.8406E+00 2.2661E+00 1.7080E+00
8.0000E+01 | 2.2203E+00 1.7596E+00 1.3235E+00 9.2488E-01
8.5000E+01 | 1.3981E+00 1.0534E+00 7.4380E-01 4.7920E-01
9.0000E+01 | 8.5941E-01 6.1393E-01 4.0558E-01 2.3986E-01
9.5000E+01 | 5.1846E-01 3.5040E-01 2.1600E-01 1.1686E-01
1.0000E+02 | 3.0824E-01 1.9677E-01 1.1294E-01 5.5750E-02
Rho
---
Stock Price | Time to Maturity (months)
| 5.0000E+00 4.5000E+00 4.0000E+00 3.5000E+00
-----------------------------------------------------------------
0.0000E+00 | 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00
5.0000E+00 | 6.3524E-18 6.5717E-20 2.2112E-22 1.4997E-25
1.0000E+01 | 5.6040E-09 5.5594E-10 3.1558E-11 8.0937E-13
1.5000E+01 | 3.6414E-05 9.3595E-06 1.7459E-06 2.0663E-07
2.0000E+01 | 4.3690E-03 1.8706E-03 6.6008E-04 1.7721E-04
2.5000E+01 | 7.9884E-02 4.6268E-02 2.3805E-02 1.0371E-02
3.0000E+01 | 5.1594E-01 3.6026E-01 2.3399E-01 1.3743E-01
3.5000E+01 | 1.7715E+00 1.3907E+00 1.0448E+00 7.3907E-01
4.0000E+01 | 4.0509E+00 3.4193E+00 2.8095E+00 2.2269E+00
4.5000E+01 | 7.0648E+00 6.2263E+00 5.3932E+00 4.5679E+00
5.0000E+01 | 1.0249E+01 9.2505E+00 8.2458E+00 7.2346E+00
5.5000E+01 | 1.3108E+01 1.1967E+01 1.0810E+01 9.6342E+00
6.0000E+01 | 1.5384E+01 1.4101E+01 1.2790E+01 1.1446E+01
6.5000E+01 | 1.7041E+01 1.5617E+01 1.4153E+01 1.2646E+01
7.0000E+01 | 1.8167E+01 1.6613E+01 1.5013E+01 1.3363E+01
7.5000E+01 | 1.8894E+01 1.7231E+01 1.5521E+01 1.3761E+01
8.0000E+01 | 1.9344E+01 1.7597E+01 1.5806E+01 1.3969E+01
8.5000E+01 | 1.9615E+01 1.7807E+01 1.5959E+01 1.4072E+01
9.0000E+01 | 1.9774E+01 1.7924E+01 1.6039E+01 1.4122E+01
9.5000E+01 | 1.9865E+01 1.7987E+01 1.6080E+01 1.4145E+01
1.0000E+02 | 1.9917E+01 1.8022E+01 1.6101E+01 1.4156E+01
- 6〜29行目には株価と満期までの期間に対応したオプションの値が出力されています。
- 33〜56行目には株価と満期までの期間に対応したThetaの値が出力されています。
- 60〜83行目には株価と満期までの期間に対応したDeltaの値が出力されています。
- 87〜110行目には株価と満期までの期間に対応したGammaの値が出力されています。
- 114〜137行目には株価と満期までの期間に対応したLambdaの値が出力されています。
- 141〜164行目には株価と満期までの期間に対応したRhoの値が出力されています。
ソースコード
(本ルーチンの詳細はd03ndf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
! D03NDF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
MODULE d03ndfe_mod
! D03NDF Example Program Module:
! Parameters and User-defined Routines
! .. Use Statements ..
USE nag_library, ONLY : nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
CONTAINS
SUBROUTINE print_greek(ns,nt,tmat,s,t,grname,greek)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: tmat
INTEGER, INTENT (IN) :: ns, nt
CHARACTER (*), INTENT (IN) :: grname
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: greek(ns,nt), s(ns), t(nt)
! .. Local Scalars ..
INTEGER :: i, j
! .. Intrinsic Functions ..
INTRINSIC len
! .. Executable Statements ..
WRITE (nout,*)
WRITE (nout,*) grname
WRITE (nout,*) ('-',i=1,len(grname))
WRITE (nout,*) ' Stock Price | Time to Maturity (months)'
WRITE (nout,99999) '|', (12.0_nag_wp*(tmat-t(i)),i=1,nt)
WRITE (nout,*) ' -----------------', ('------------',i=1,nt)
DO i = 1, ns
WRITE (nout,99998) s(i), '|', (greek(i,j),j=1,nt)
END DO
RETURN
99999 FORMAT (16X,A,1X,12(1P,E12.4))
99998 FORMAT (1X,1P,E12.4,3X,A,1X,12(1P,E12.4))
END SUBROUTINE print_greek
END MODULE d03ndfe_mod
PROGRAM d03ndfe
! D03NDF Example Main Program
! .. Use Statements ..
USE nag_library, ONLY : d03ndf, nag_wp
USE d03ndfe_mod, ONLY : nin, nout, print_greek
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
LOGICAL, PARAMETER :: gprnt(5) = .TRUE.
! .. Local Scalars ..
REAL (KIND=nag_wp) :: ds, dt, tmat, x
INTEGER :: i, ifail, j, kopt, ns, nt
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: delta(:,:), f(:,:), gamma(:,:), &
lambda(:,:), rho(:,:), s(:), &
t(:), theta(:,:)
REAL (KIND=nag_wp) :: q(3), r(3), sigma(3)
LOGICAL :: tdpar(3)
! .. Intrinsic Functions ..
INTRINSIC real
! .. Executable Statements ..
WRITE (nout,*) 'D03NDF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
READ (nin,*) ns, nt
ALLOCATE (delta(ns,nt),f(ns,nt),gamma(ns,nt),lambda(ns,nt),rho(ns,nt), &
s(ns),t(nt),theta(ns,nt))
! Read problem parameters
READ (nin,*) kopt
READ (nin,*) x
READ (nin,*) tmat
READ (nin,*) q(1), r(1), sigma(1)
READ (nin,*) s(1), s(ns)
READ (nin,*) t(1), t(nt)
READ (nin,*) tdpar(1:3)
IF (ns<2) THEN
WRITE (nout,*) 'NS invalid.'
ELSE IF (nt<2) THEN
WRITE (nout,*) 'NT invalid.'
ELSE
ds = (s(ns)-s(1))/real(ns-1,kind=nag_wp)
dt = (t(nt)-t(1))/real(nt-1,kind=nag_wp)
! Loop over times
DO j = 1, nt
t(j) = t(1) + real(j-1,kind=nag_wp)*dt
! Loop over stock prices
DO i = 1, ns
s(i) = s(1) + real(i-1,kind=nag_wp)*ds
! Call Black-Scholes solver
ifail = 0
CALL d03ndf(kopt,x,s(i),t(j),tmat,tdpar,r,q,sigma,f(i,j), &
theta(i,j),delta(i,j),gamma(i,j),lambda(i,j),rho(i,j), &
ifail)
END DO
END DO
! Output option values and possibly Greeks.
CALL print_greek(ns,nt,tmat,s,t,'Option Values',f)
IF (gprnt(1)) CALL print_greek(ns,nt,tmat,s,t,'Theta',theta)
IF (gprnt(2)) CALL print_greek(ns,nt,tmat,s,t,'Delta',delta)
IF (gprnt(3)) CALL print_greek(ns,nt,tmat,s,t,'Gamma',gamma)
IF (gprnt(4)) CALL print_greek(ns,nt,tmat,s,t,'Lambda',lambda)
IF (gprnt(5)) CALL print_greek(ns,nt,tmat,s,t,'Rho',rho)
END IF
END PROGRAM d03ndfe
