Keyword: 後退差分公式, 常微分方程式
概要
本サンプルは後退差分公式を用いた常微分方程式を求めるFortranによるサンプルプログラムです。 本サンプルは以下に示される常微分方程式について5つのケースの計算をし、出力します。
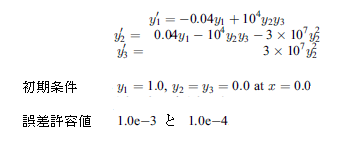
※本サンプルはnAG Fortranライブラリに含まれるルーチン d02ejf() のExampleコードです。本サンプル及びルーチンの詳細情報は d02ejf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はd02ejf のマニュアルページを参照)- 1行目はタイトル行で読み飛ばされます。
- 2行目は独立変数xの初期値(xinit)と最終値(xned)を指定しています。
- 3行目は解の初期値(yinit)を指定しています。
- 4行目は独立変数xの刻み幅の値の数(kinit)を指定しています。
出力結果
(本ルーチンの詳細はd02ejf のマニュアルページを参照)| この出力例をダウンロード |
D02EJF Example Program Results
Case 1: calculating Jacobian internally,
intermediate output, root-finding
Calculation with TOL = 0.1E-02
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94163 0.00003 0.05834
4.00 0.90551 0.00002 0.09447
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Calculation with TOL = 0.1E-03
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94161 0.00003 0.05837
4.00 0.90551 0.00002 0.09446
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Case 2: calculating Jacobian by PEDERV,
intermediate output, root-finding
Calculation with TOL = 0.1E-02
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94163 0.00003 0.05834
4.00 0.90551 0.00002 0.09447
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Calculation with TOL = 0.1E-03
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94161 0.00003 0.05837
4.00 0.90551 0.00002 0.09446
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Case 3: calculating Jacobian internally,
no intermediate output, root-finding
Calculation with TOL = 0.1E-02
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Calculation with TOL = 0.1E-03
Root of Y(1)-0.9 at 4.377
Solution is 0.90000 0.00002 0.09998
Case 4: calculating Jacobian internally,
intermediate output, no root-finding
Calculation with TOL = 0.1E-02
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94163 0.00003 0.05834
4.00 0.90551 0.00002 0.09447
6.00 0.87930 0.00002 0.12068
8.00 0.85858 0.00002 0.14140
10.00 0.84136 0.00002 0.15862
Calculation with TOL = 0.1E-03
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
2.00 0.94161 0.00003 0.05837
4.00 0.90551 0.00002 0.09446
6.00 0.87926 0.00002 0.12072
8.00 0.85854 0.00002 0.14145
10.00 0.84136 0.00002 0.15863
Case 5: calculating Jacobian internally,
no intermediate output, no root-finding (integrate to XEND)
Calculation with TOL = 0.1E-02
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
10.00 0.84136 0.00002 0.15862
Calculation with TOL = 0.1E-03
X Y(1) Y(2) Y(3)
0.00 1.00000 0.00000 0.00000
10.00 0.84136 0.00002 0.15863
- 3〜20行目にはケース1の結果が出力されています。ケース1ではy=0.9となるデータ点が見つかるまで 2.0の間隔でx=10.0まで計算を行い、中間結果を出力しています。ヤコビ行列を数値的に計算しています。
- 6〜10行目にxの値と許容値 0.1e-002 で計算したyの値が出力されています。
- 11行目にy=0.9となるデータ点が出力されています。
- 12行目に常微分方程式の解が出力されています。
- 14〜18行目にxの値と許容値 0.1e-003 で計算したyの値が出力されています。
- 19行目にy=0.9となるデータ点が出力されています。
- 20行目に常微分方程式の解が出力されています。
- 23〜40行目にはケース2の結果が出力されています。ケース2ではケース1と同様の計算を行い、中間結果を出力し解が見つかったら終了します。ヤコビ行列を分析的に計算しています。
- 43〜52行目にケース3の結果が出力されています。ケース3ではケース1と同様の計算を行いますが、中間結果の出力を行わず、解が見つかったら終了します。
- 55〜74行目にケース4の結果が出力されています。ケース4ではケース1と同様の計算を行いますが、中間結果を出力し、x=10.0まで計算を行っています。
- 77〜88行目にケース5の結果が出力されています。ケース5ではケース1と同様の計算を行いますが中間結果の出力を行わず、x=10.0まで計算を行っています。
ソースコード
(本ルーチンの詳細はd02ejf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
! D02EJF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
MODULE d02ejfe_mod
! Data for D02EJF example program
! .. Use Statements ..
USE nag_library, ONLY : nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
REAL (KIND=nag_wp), PARAMETER :: alpha = 0.04_nag_wp
REAL (KIND=nag_wp), PARAMETER :: beta = 1.0E4_nag_wp
REAL (KIND=nag_wp), PARAMETER :: gamma = 3.0E7_nag_wp
REAL (KIND=nag_wp), PARAMETER :: zero = 0.0_nag_wp
INTEGER, PARAMETER :: n = 3, nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: h, xend
INTEGER, SAVE :: k
CONTAINS
SUBROUTINE fcn(x,y,f)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: x
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: f(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(*)
! .. Executable Statements ..
f(1) = -alpha*y(1) + beta*y(2)*y(3)
f(2) = alpha*y(1) - beta*y(2)*y(3) - gamma*y(2)*y(2)
f(3) = gamma*y(2)*y(2)
RETURN
END SUBROUTINE fcn
SUBROUTINE pederv(x,y,pw)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: x
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: pw(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(*)
! .. Executable Statements ..
pw(1) = -alpha
pw(2) = alpha
pw(3) = zero
pw(4) = beta*y(3)
pw(5) = -beta*y(3) - 2.0_nag_wp*gamma*y(2)
pw(6) = 2.0_nag_wp*gamma*y(2)
pw(7) = beta*y(2)
pw(8) = -beta*y(2)
pw(9) = zero
RETURN
END SUBROUTINE pederv
FUNCTION g(x,y)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Function Return Value ..
REAL (KIND=nag_wp) :: g
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: x
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: y(*)
! .. Executable Statements ..
g = y(1) - 0.9E0_nag_wp
RETURN
END FUNCTION g
SUBROUTINE output(xsol,y)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (INOUT) :: xsol
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: y(*)
! .. Local Scalars ..
INTEGER :: j
! .. Intrinsic Functions ..
INTRINSIC real
! .. Executable Statements ..
WRITE (nout,99999) xsol, (y(j),j=1,n)
xsol = xend - real(k,kind=nag_wp)*h
k = k - 1
RETURN
99999 FORMAT (1X,F8.2,3F13.5)
END SUBROUTINE output
END MODULE d02ejfe_mod
PROGRAM d02ejfe
! D02EJF Example Main Program
! .. Use Statements ..
USE nag_library, ONLY : d02ejf, d02ejw, d02ejx, d02ejy, nag_wp
USE d02ejfe_mod, ONLY : fcn, g, h, k, n, nin, nout, output, pederv, xend
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
REAL (KIND=nag_wp) :: tol, x, xinit
INTEGER :: i, icase, ifail, iw, j, kinit
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: w(:), y(:), yinit(:)
! .. Intrinsic Functions ..
INTRINSIC real
! .. Executable Statements ..
WRITE (nout,*) 'D02EJF Example Program Results'
iw = (12+n)*n + 50
ALLOCATE (w(iw),y(n),yinit(n))
! Skip heading in data file
READ (nin,*)
! xinit: initial x value, xend: final x value
! y: initial solution values
READ (nin,*) xinit, xend
READ (nin,*) yinit(1:n)
READ (nin,*) kinit
DO icase = 1, 5
IF (icase/=2) THEN
WRITE (nout,99995) icase, 'Jacobian internally'
ELSE
WRITE (nout,99995) icase, 'Jacobian by PEDERV'
END IF
SELECT CASE (icase)
CASE (1,2)
WRITE (nout,99994) 'intermediate output, root-finding'
CASE (3)
WRITE (nout,99994) 'no intermediate output, root-finding'
CASE (4)
WRITE (nout,99994) 'intermediate output, no root-finding'
CASE (5)
WRITE (nout,99994) &
'no intermediate output, no root-finding (integrate to XEND)'
END SELECT
DO j = 3, 4
tol = 10.0E0_nag_wp**(-j)
WRITE (nout,99999) ' Calculation with TOL =', tol
x = xinit
y(1:n) = yinit(1:n)
IF (icase/=3) THEN
WRITE (nout,*) ' X Y(1) Y(2) Y(3)'
k = kinit
h = (xend-x)/real(k+1,kind=nag_wp)
END IF
ifail = 0
SELECT CASE (icase)
CASE (1)
CALL d02ejf(x,xend,n,y,fcn,d02ejy,tol,'Default',output,g,w,iw, &
ifail)
WRITE (nout,99998) ' Root of Y(1)-0.9 at', x
WRITE (nout,99997) ' Solution is', (y(i),i=1,n)
CASE (2)
CALL d02ejf(x,xend,n,y,fcn,pederv,tol,'Default',output,g,w,iw, &
ifail)
WRITE (nout,99998) ' Root of Y(1)-0.9 at', x
WRITE (nout,99997) ' Solution is', (y(i),i=1,n)
CASE (3)
CALL d02ejf(x,xend,n,y,fcn,d02ejy,tol,'Default',d02ejx,g,w,iw, &
ifail)
WRITE (nout,99998) ' Root of Y(1)-0.9 at', x
WRITE (nout,99997) ' Solution is', (y(i),i=1,n)
CASE (4)
ifail = 0
CALL d02ejf(x,xend,n,y,fcn,d02ejy,tol,'Default',output,d02ejw, &
w,iw,ifail)
CASE (5)
WRITE (nout,99996) x, (y(i),i=1,n)
CALL d02ejf(x,xend,n,y,fcn,d02ejy,tol,'Default',d02ejx,d02ejw, &
w,iw,ifail)
WRITE (nout,99996) x, (y(i),i=1,n)
END SELECT
IF (tol<0.0E0_nag_wp) WRITE (nout,*) ' Range too short for TOL'
END DO
IF (icase<5) THEN
WRITE (nout,*)
END IF
END DO
99999 FORMAT (/1X,A,E8.1)
99998 FORMAT (1X,A,F7.3)
99997 FORMAT (1X,A,3F13.5)
99996 FORMAT (1X,F8.2,3F13.5)
99995 FORMAT (/1X,'Case ',I1,': calculating ',A,',')
99994 FORMAT (8X,A)
END PROGRAM d02ejfe
