Keyword: 階層的クラスター分析, 多変量解析
概要
本サンプルは階層的クラスター分析を行うFortranによるサンプルプログラムです。 本サンプルは以下に示されるオブジェクトについて階層的クラスター分析を行い、クラスターの距離と結合されたクラスターを出力します。
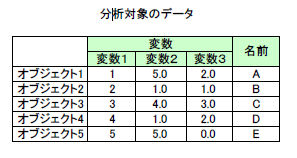
※本サンプルはnAG Fortranライブラリに含まれるルーチン g03ecf() のExampleコードです。本サンプル及びルーチンの詳細情報は g03ecf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はg03ecf のマニュアルページを参照)| このデータをダウンロード |
G03ECF Example Program Data 5 3 : N,M (G03EAF) 'I' 'S' 'U' : UPDATE,DIST,SCAL (G03EAF) 1 5.0 2.0 2 1.0 1.0 3 4.0 3.0 4 1.0 2.0 5 5.0 0.0 : End of X (G03EAF) 0 1 1 : ISX (G03EAF) 5 : METHOD (G03ECF) 'A' 'B' 'C' 'D' 'E' : Row names (ROW_NAME)
- 1行目はタイトル行で読み飛ばされます。
- 2行目にオブジェクトの数(n)と変数の総数(m)を指定しています。
- 3行目には既存の距離行列がアップデートされるかを示すパラメータ(update='I')、どの種類の距離が計算されるかを示すパラメータ(dist='S')、変数の標準化を示すパラメータ(scal='U')を指定しています。
この場合、"I" は距離が距離行列に追加される前に行列がゼロに初期化されることを意味しています。 "S" はユークリッド平方距離が計算されることを意味しています。"U" は変数がスケーリングされないことを意味しています。 - 4〜8行目にオブジェクトに対する変数の値(x)を指定しています。
- 9行目に変数が距離計算に含まれるかどうかのフラグ(isx)を指定しています。
- 10行目にクラスタリングの手法(method)を指定しています。"5"はメディアン法を意味しています。
- 11行目にはオブジェクトに対する名前(row_name)を指定しています。
出力結果
(本ルーチンの詳細はg03ecf のマニュアルページを参照)| この出力例をダウンロード |
G03ECF Example Program Results
Distance Clusters Joined
1.000 B D
2.000 A C
6.500 A E
14.125 A B
- 5〜8行目にクラスターの距離と結合されたクラスターが出力されています。
ソースコード
(本ルーチンの詳細はg03ecf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM g03ecfe
! G03ECF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : g03eaf, g03ecf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6, rnlen = 3
! .. Local Scalars ..
INTEGER :: i, ifail, ld, ldx, liwk, m, method, &
n, n1
CHARACTER (1) :: dist, scal, update
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: cd(:), d(:), dord(:), s(:), x(:,:)
INTEGER, ALLOCATABLE :: ilc(:), iord(:), isx(:), iuc(:), &
iwk(:)
CHARACTER (rnlen), ALLOCATABLE :: row_name(:)
! .. Executable Statements ..
WRITE (nout,*) 'G03ECF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in the problem size
READ (nin,*) n, m
! Read in information on the type of distance matrix to use
READ (nin,*) update, dist, scal
ldx = n
ld = n*(n-1)/2
n1 = n - 1
liwk = 2*n
ALLOCATE (x(ldx,m),isx(m),s(m),d(ld),ilc(n1),iuc(n1),cd(n1),iord(n), &
dord(n),iwk(liwk),row_name(n))
! Read in the data used to construct distance matrix
READ (nin,*) (x(i,1:m),i=1,n)
! Read in variable inclusion flags
READ (nin,*) isx(1:m)
! Read in scaling
IF (scal=='G' .OR. scal=='g') THEN
READ (nin,*) s(1:m)
END IF
! Compute the distance matrix
ifail = 0
CALL g03eaf(update,dist,scal,n,m,x,ldx,isx,s,d,ifail)
! Read in information on the clustering method to use
READ (nin,*) method
! Read in first RNLEN characters of row names. Used to make example
! output easier to read
READ (nin,*) row_name(1:n)
! Perform clustering
ifail = 0
CALL g03ecf(method,n,d,ilc,iuc,cd,iord,dord,iwk,ifail)
! Display results
WRITE (nout,*) ' Distance Clusters Joined'
WRITE (nout,*)
WRITE (nout,99999) (cd(i),row_name(ilc(i)),row_name(iuc(i)),i=1,n1)
99999 FORMAT (F10.3,5X,2A)
END PROGRAM g03ecfe
