Keyword: 平方根共分散フィルタ, カルマンフィルタ, 観測更新, 時間更新
概要
本サンプルは平方根共分散フィルタを用いた時不変カルマンフィルタの観測更新と時間更新を行うFortranによるサンプルプログラムです。 本サンプルでは以下に示される入力データを読み込み、更新ごとの観測ベクトルの残差や最後の更新後の状態ベクトルの推定値を出力します。
※本サンプルはnAG Fortranライブラリに含まれるルーチン g13ebf() のExampleコードです。本サンプル及びルーチンの詳細情報は
g13ebf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はg13ebf のマニュアルページを参照)| このデータをダウンロード |
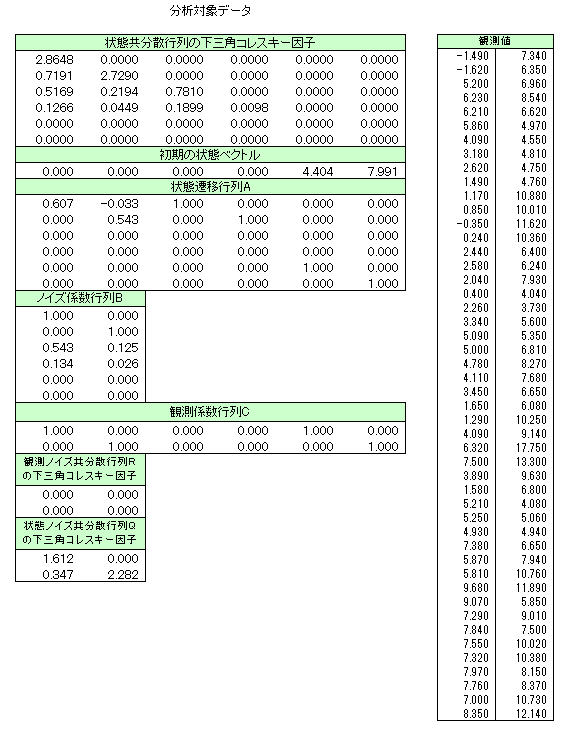
G13EBF Example Program Data 6 2 2 F :: N,M,L,STQ 2.8648 0.0000 0.0000 0.0000 0.0000 0.0000 0.7191 2.7290 0.0000 0.0000 0.0000 0.0000 0.5169 0.2194 0.7810 0.0000 0.0000 0.0000 0.1266 0.0449 0.1899 0.0098 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 :: End of S F :: FULL flag for S 0.000 0.000 0.000 0.000 4.404 7.991 :: AX 0.607 -0.033 1.000 0.000 0.000 0.000 0.000 0.543 0.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 :: End of A 1.000 0.000 0.000 1.000 0.543 0.125 0.134 0.026 0.000 0.000 0.000 0.000 :: End of B 1.000 0.000 0.000 0.000 1.000 0.000 0.000 1.000 0.000 0.000 0.000 1.000 :: End of C 0.000 0.000 0.000 0.000 :: End of R F :: FULL flag for R 1.612 0.000 0.347 2.282 :: End of Q F :: FULL flag for Q 48 0.0 :: NCALL,TOL -1.490 7.340 -1.620 6.350 5.200 6.960 6.230 8.540 6.210 6.620 5.860 4.970 4.090 4.550 3.180 4.810 2.620 4.750 1.490 4.760 1.170 10.880 0.850 10.010 -0.350 11.620 0.240 10.360 2.440 6.400 2.580 6.240 2.040 7.930 0.400 4.040 2.260 3.730 3.340 5.600 5.090 5.350 5.000 6.810 4.780 8.270 4.110 7.680 3.450 6.650 1.650 6.080 1.290 10.250 4.090 9.140 6.320 17.750 7.500 13.300 3.890 9.630 1.580 6.800 5.210 4.080 5.250 5.060 4.930 4.940 7.380 6.650 5.870 7.940 5.810 10.760 9.680 11.890 9.070 5.850 7.290 9.010 7.840 7.500 7.550 10.020 7.320 10.380 7.970 8.150 7.760 8.370 7.000 10.730 8.350 12.140 :: End of Y
- 1行目はタイトル行で読み飛ばされます。
- 2行目に状態ベクトルのサイズ(n=6)、観測ベクトルのサイズ(m=2)、状態ノイズの次数(l=2)、状態ノイズ共分散行列が恒等行列と仮定されるかどうか(stq=F)を指定しています。"F"は下三角コレスキー因子が行列Qで提供されることを意味しています。
- 3〜8行目は状態共分散行列Sの下三角コレスキー因子(s)を指定しています。
- 9行目は行列Sがフル行列かどうか(full)を指定しています。"F"はフル行列を意味しています。
- 10行目は初期の状態ベクトル(ax)を指定しています。
- 11〜16行目は状態遷移行列Aを指定しています。
- 17〜22行目はノイズ係数行列Bを指定しています。
- 23〜24行目は観測係数行列Cを指定しています。
- 25〜26行目は観測ノイズ共分散行列Rの下三角コレスキー因子(r)を指定しています。
- 27行目は行列Rがフル行列かコレスキー分解かどうか(full)を指定しています。"F"はフル行列を意味しています。
- 28〜29行目は状態ノイズ共分散行列Qの下三角コレスキー因子(q)を指定しています。
- 30行目は行列Qがフル行列かコレスキー分解かどうか(full)を指定しています。"F"はフル行列を意味しています。
- 31行目は呼び出し回数(ncall=48)と特異性検定のための許容値(tol=0.0)を指定しています。
- 32〜79行目は観測値(y)を指定しています。
出力結果
(本ルーチンの詳細はg13ebf のマニュアルページを参照)| この出力例をダウンロード |
G13EBF Example Program Results
Residuals
-5.8940 -0.6510
-1.4710 -1.0407
5.1658 0.0447
-1.3281 0.4580
1.3653 -1.5066
-0.2337 -2.4192
-0.8685 -1.7065
-0.4624 -1.1519
-0.7510 -1.4218
-1.3526 -1.3335
-0.6707 4.8593
-1.7389 0.4138
-1.6376 2.7549
-0.6137 0.5463
0.9067 -2.8093
-0.8255 -0.9355
-0.7494 1.0247
-2.2922 -3.8441
1.8812 -1.7085
-0.7112 -0.2849
1.6747 -1.2400
-0.6619 0.0609
0.3271 1.0074
-0.8165 -0.5325
-0.2759 -1.0489
-1.9383 -1.1186
-0.3131 3.5855
1.3726 -0.1289
1.4153 8.9545
0.3672 -0.4126
-2.3659 -1.2823
-1.0130 -1.7306
3.2472 -3.0836
-1.1501 -1.1623
0.6855 -1.2751
2.3432 0.2570
-1.6892 0.3565
1.3871 3.0138
3.3840 2.1312
-0.5118 -4.7670
0.8569 2.3741
0.9558 -1.2209
0.6778 2.1993
0.4304 1.1393
1.4987 -1.2255
0.5361 0.1237
0.2649 2.4582
2.0095 2.5623
Final X(I+1:I)
3.6698 2.5888 0.0000 0.0000 4.4040 7.9910
Final Value of P
1 2 3 4 5
1 2.5985E+00
2 5.5936E-01 5.3279E+00
3 1.4809E+00 9.6973E-01 9.2536E-01
4 3.6275E-01 2.1348E-01 2.2366E-01 5.4159E-02
5 -4.0547E-16 -8.7283E-17 -2.3108E-16 -5.6603E-17 9.6581E-32
6 4.4742E-17 9.6312E-18 2.5499E-17 6.2458E-18 -9.3231E-33
6
1
2
3
4
5
6 1.3378E-32
Deviance = 0.2229E+03
- 5〜52行目までは更新ごとの観測ベクトルの残差が出力されています。
- 55行目は最後の更新後の状態ベクトルの推定値が出力されています。
- 59〜72行目は最後の更新後の状態共分散行列が出力されています。
- 73行目はデビアンス(deviance)が出力されています。
ソースコード
(本ルーチンの詳細はg13ebf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM g13ebfe
! G13EBF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : ddot, dgemv, dpotrf, dsyrk, dtrsv, g13ebf, &
nag_wp, x04caf
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
REAL (KIND=nag_wp), PARAMETER :: one = 1.0_nag_wp
REAL (KIND=nag_wp), PARAMETER :: zero = 0.0_nag_wp
INTEGER, PARAMETER :: inc1 = 1, nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: dev, tol
INTEGER :: i, ifail, info, istep, l, ldm, ldq, &
lds, lwk, m, n, ncall, tdq
LOGICAL :: full, stq
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), ax(:), b(:,:), c(:,:), &
h(:,:), k(:,:), p(:,:), q(:,:), &
r(:,:), s(:,:), u(:,:), us(:,:), &
wk(:), x(:), y(:)
INTEGER, ALLOCATABLE :: iwk(:)
! .. Intrinsic Functions ..
INTRINSIC log
! .. Executable Statements ..
WRITE (nout,*) 'G13EBF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in problem size
READ (nin,*) n, m, l, stq
lds = n
IF ( .NOT. stq) THEN
ldq = l
tdq = l
ELSE
ldq = 1
tdq = 1
END IF
ldm = m
lwk = (n+m)*(n+m+l)
ALLOCATE (a(lds,n),b(lds,l),q(ldq,tdq),c(ldm,n),r(ldm,m),s(lds,n), &
k(lds,m),h(ldm,m),u(lds,n),iwk(m),wk(lwk),ax(n),y(m),x(n),p(lds,n), &
us(lds,n))
! Read in the state covariance matrix, S
READ (nin,*) (s(i,1:n),i=1,n)
! Read in flag indicating whether S is the full matrix, or its
! Cholesky decomposition.
READ (nin,*) full
! If required, perform Cholesky decomposition on S
IF (full) THEN
! The nAG name equivalent of dpotrf is f07fdf
CALL dpotrf('L',n,s,lds,info)
IF (info>0) THEN
WRITE (nout,*) ' S not positive definite'
GO TO 20
END IF
END IF
! Read in initial state vector
READ (nin,*) ax(1:n)
! Read in transition matrix, A
READ (nin,*) (a(i,1:n),i=1,n)
! Read in noise coefficient matrix, B
READ (nin,*) (b(i,1:l),i=1,n)
! Read in measurement coefficient matrix, C
READ (nin,*) (c(i,1:n),i=1,m)
! Read in measurement noise covariance matrix, R
READ (nin,*) (r(i,1:m),i=1,m)
! Read in flag indicating whether R is the full matrix, or its Cholesky
! decomposition
READ (nin,*) full
! If required, perform Cholesky decomposition on R
IF (full) THEN
! The nAG name equivalent of dpotrf is f07fdf
CALL dpotrf('L',m,r,ldm,info)
IF (info>0) THEN
WRITE (nout,*) ' R not positive definite'
GO TO 20
END IF
END IF
! Read in state noise matrix Q, if not assume to be identity matrix
IF ( .NOT. stq) THEN
READ (nin,*) (q(i,1:l),i=1,l)
! Read in flag indicating whether Q is the full matrix, or
! its Cholesky decomposition
READ (nin,*) full
! Perform cholesky factorisation on Q, if full matrix is supplied
IF (full) THEN
! The nAG name equivalent of dpotrf is f07fdf
CALL dpotrf('L',l,q,ldq,info)
IF (info>0) THEN
WRITE (nout,*) ' Q not positive definite'
GO TO 20
END IF
END IF
END IF
! Read in control parameters
READ (nin,*) ncall, tol
! Display titles
WRITE (nout,*) ' Residuals'
WRITE (nout,*)
! Loop through data
dev = 0.0E0_nag_wp
DO istep = 1, ncall
! Read in observed values
READ (nin,*) y(1:m)
IF (istep==1) THEN
! Make first call to G13EBF
ifail = 0
CALL g13ebf('T',n,m,l,a,lds,b,stq,q,ldq,c,ldm,r,s,k,h,u,tol,iwk, &
wk,ifail)
! The nAG name equivalent of dgemv is f06paf
CALL dgemv('N',n,n,one,u,lds,ax,inc1,zero,x,inc1)
ELSE
! Make remaining calls to G13EBF
ifail = 0
CALL g13ebf('H',n,m,l,a,lds,b,stq,q,ldq,c,ldm,r,s,k,h,u,tol,iwk, &
wk,ifail)
END IF
! Perform time and measurement update x <= Ax + K(y-Cx)
! The nAG name equivalent of dgemv is f06paf
CALL dgemv('N',m,n,-one,c,ldm,x,inc1,one,y,inc1)
CALL dgemv('N',n,n,one,a,lds,x,inc1,zero,ax,inc1)
CALL dgemv('N',n,m,one,k,lds,y,inc1,one,ax,inc1)
x(1:n) = ax(1:n)
! Display the residuals
WRITE (nout,99999) y(1:m)
! Update loglikelihood
! The nAG name equivalent of dtrsv is f06pjf
CALL dtrsv('L','N','N',m,h,ldm,y,inc1)
! The nAG name equivalent of ddot is f06eaf
dev = dev + ddot(m,y,1,y,1)
DO i = 1, m
dev = dev + 2.0_nag_wp*log(h(i,i))
END DO
END DO
! Calculate back-transformed x <- U^T x
! The nAG name equivalent of dgemv is f06paf
CALL dgemv('T',n,n,one,u,lds,ax,inc1,zero,x,inc1)
! Compute back-transformed P from S
DO i = 1, n
CALL dgemv('T',n-i+1,n,one,u(i,1),lds,s(i,i),inc1,zero,us(1,i),inc1)
END DO
! The nAG name equivalent of dsyrk is f06ypf
CALL dsyrk('L','N',n,n,one,us,lds,zero,p,lds)
! Display final results
WRITE (nout,*)
WRITE (nout,*) ' Final X(I+1:I) '
WRITE (nout,99999) x(1:n)
WRITE (nout,*)
FLUSH (nout)
ifail = 0
CALL x04caf('Lower','N',n,n,p,lds,'Final Value of P',ifail)
WRITE (nout,99998) ' Deviance = ', dev
20 CONTINUE
99999 FORMAT (6F12.4)
99998 FORMAT (A,E13.4)
END PROGRAM g13ebfe
