Keyword: 一変量, GJR, GARCH, 非対称, パラメータ推定
概要
本サンプルは一変量の非対称なGJR GARCHプロセスのパラメータ推定を行うFortranによるサンプルプログラムです。 本サンプルでは以下に示される時系列を分析対象とし下記の式で表されるGJR GARCHプロセスのパラメータ推定を行います。
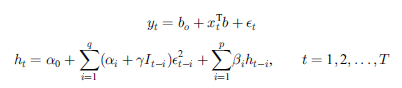
※本サンプルはnAG Fortranライブラリに含まれるルーチン g13fef() のExampleコードです。本サンプル及びルーチンの詳細情報は g13fef のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
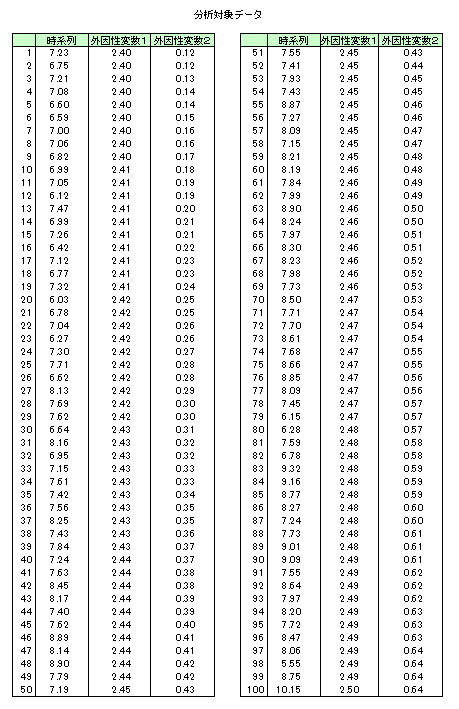
入力データ
(本ルーチンの詳細はg13fef のマニュアルページを参照)| このデータをダウンロード |
G13FEF Example Program Data 100 1 2 :: NUM,MN,NREG 7.23 6.75 7.21 7.08 6.60 6.59 7.00 7.06 6.82 6.99 7.05 6.12 7.47 6.99 7.26 6.42 7.12 6.77 7.32 6.03 6.78 7.04 6.27 7.30 7.71 6.62 8.13 7.69 7.62 6.64 8.16 6.95 7.15 7.61 7.42 7.56 8.25 7.43 7.84 7.24 7.63 8.45 8.17 7.40 7.62 8.89 8.14 8.90 7.79 7.19 7.55 7.41 7.93 7.43 8.87 7.27 8.09 7.15 8.21 8.19 7.84 7.99 8.90 8.24 7.97 8.30 8.23 7.98 7.73 8.50 7.71 7.70 8.61 7.68 8.66 8.85 8.09 7.45 6.15 6.28 7.59 6.78 9.32 9.16 8.77 8.27 7.24 7.73 9.01 9.09 7.55 8.64 7.97 8.20 7.72 8.47 8.06 5.55 8.75 10.15 :: End of Y 2.40 0.12 2.40 0.12 2.40 0.13 2.40 0.14 2.40 0.14 2.40 0.15 2.40 0.16 2.40 0.16 2.40 0.17 2.41 0.18 2.41 0.19 2.41 0.19 2.41 0.20 2.41 0.21 2.41 0.21 2.41 0.22 2.41 0.23 2.41 0.23 2.41 0.24 2.42 0.25 2.42 0.25 2.42 0.26 2.42 0.26 2.42 0.27 2.42 0.28 2.42 0.28 2.42 0.29 2.42 0.30 2.42 0.30 2.43 0.31 2.43 0.32 2.43 0.32 2.43 0.33 2.43 0.33 2.43 0.34 2.43 0.35 2.43 0.35 2.43 0.36 2.43 0.37 2.44 0.37 2.44 0.38 2.44 0.38 2.44 0.39 2.44 0.39 2.44 0.40 2.44 0.41 2.44 0.41 2.44 0.42 2.44 0.42 2.45 0.43 2.45 0.43 2.45 0.44 2.45 0.45 2.45 0.45 2.45 0.46 2.45 0.46 2.45 0.47 2.45 0.47 2.45 0.48 2.46 0.48 2.46 0.49 2.46 0.49 2.46 0.50 2.46 0.50 2.46 0.51 2.46 0.51 2.46 0.52 2.46 0.52 2.46 0.53 2.47 0.53 2.47 0.54 2.47 0.54 2.47 0.54 2.47 0.55 2.47 0.55 2.47 0.56 2.47 0.56 2.47 0.57 2.47 0.57 2.48 0.57 2.48 0.58 2.48 0.58 2.48 0.59 2.48 0.59 2.48 0.59 2.48 0.60 2.48 0.60 2.48 0.61 2.48 0.61 2.49 0.61 2.49 0.62 2.49 0.62 2.49 0.62 2.49 0.63 2.49 0.63 2.49 0.63 2.49 0.64 2.49 0.64 2.49 0.64 2.50 0.64 :: End of X 'T' 1 1 :: DIST,IP,IQ T T 200 0.00001 :: COPTS,MAXIT,TOL 0.025 :: ALPHA_0 0.050 :: ALPHA_I 0.400 :: BETA_I 0.045 :: GAMMA 3.250 :: DF 1.500 :: MEAN 4 :: NT
- 1行目はタイトル行で読み飛ばされます。
- 2行目に時系列のデータの数(num=100)、切片がモデルに含まれかどうか(mn=1:含まれる)、 回帰係数の数(nreg=2)を指定しています。
- 3〜22行目に時系列の観測値(y)を指定しています。
- 23〜72行目に時間依存の外因性変数の要素(x)を指定しています。
- 73行目に分布の種類(dist='T':スチューデントt分布)、係数βの数(ip=1)、係数αの数(iq=1)を指定しています。
- 74行目に定常状態が強制されるかどうか(copts(1)=T:強制される)、ルーチンが初期のパラメータ推定を与えるかどうか(copts(2)=T:与える)、最大反復数(maxit=200)、最適化ルーチンで使用される許容値(tol=0.00001)を指定しています。
- 75行目に係数α0(alpha_0)を指定しています。
- 76行目に係数α1(alpha_i)を指定しています。
- 77行目に係数β1(beta_i)を指定しています。
- 78行目に非対称パラメータγ(gamma)を指定しています。
- 79行目に自由度(df)を指定しています。
- 80行目に切片(mean)を指定しています。
- 81行目に予測期間(nt)を指定しています。
出力結果
(本ルーチンの詳細はg13fef のマニュアルページを参照)| この出力例をダウンロード |
G13FEF Example Program Results
Parameter Standard
estimates errors
Alpha0 0.08 0.12
Alpha1 0.00 0.85
Beta1 0.67 0.19
Gamma 0.35 0.63
DF 5.03 5.13
B0 50.22 3.33
B1 -18.48 1.43
B2 6.45 0.54
Volatility forecast = 0.61
- 5行目に係数α0のパラメータ推定値、標準誤差が出力されています。
- 6行目に係数α1のパラメータ推定値、標準誤差が出力されています。
- 8行目に係数β1のパラメータ推定値、標準誤差が出力されています。
- 10行目に非対称パラメータγのパラメータ推定値、標準誤差が出力されています。
- 12行目に自由度のパラメータ推定値、標準誤差が出力されています。
- 14行目に切片のパラメータ推定値、標準誤差が出力されています。
- 15〜16行目に線形回帰係数のパラメータ推定値、標準誤差が出力されています。
- 19行目には4step先のボラティリティ予測値が出力されています。
ソースコード
(本ルーチンの詳細はg13fef のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM g13fefe
! G13FEF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : g13fef, g13fff, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: gamma, hp, lgf, tol
INTEGER :: i, ifail, ip, iq, l, ldcovr, ldx, &
lwork, maxit, mn, npar, nreg, nt, &
num, pgamma, tdx
LOGICAL :: tdist
CHARACTER (1) :: dist
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: covr(:,:), et(:), fht(:), ht(:), &
sc(:), se(:), theta(:), work(:), &
x(:,:), yt(:)
LOGICAL :: copts(2)
! .. Intrinsic Functions ..
INTRINSIC max
! .. Executable Statements ..
WRITE (nout,*) 'G13FEF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in the problem size
READ (nin,*) num, mn, nreg
ldx = num
tdx = max(nreg+mn,1)
ALLOCATE (yt(num),x(ldx,tdx))
! Read in the series
READ (nin,*) yt(1:num)
! Read in the exogenous variables
IF (nreg>0) THEN
READ (nin,*) (x(i,1:nreg),i=1,num)
END IF
! Read in details of the model to fit
READ (nin,*) dist, ip, iq
! Read in control parameters
READ (nin,*) copts(1:2), maxit, tol
! Calculate NPAR
npar = 2 + iq + ip + mn + nreg
IF (dist=='T' .OR. dist=='t') THEN
npar = npar + 1
tdist = .TRUE.
ELSE
tdist = .FALSE.
END IF
ldcovr = npar
lwork = (nreg+3)*num + npar + 403
ALLOCATE (theta(npar),se(npar),sc(npar),covr(ldcovr,npar),et(num), &
ht(num),work(lwork))
! Read in initial values
! alpha_0
READ (nin,*) theta(1)
l = 2
! alpha_i
IF (iq>0) THEN
READ (nin,*) theta(l:(l+iq-1))
l = l + iq
END IF
! beta_i
IF (ip>0) THEN
READ (nin,*) theta(l:(l+ip-1))
l = l + ip
END IF
! gamma
READ (nin,*) theta(l)
pgamma = l
l = l + 1
! degrees of freedom
IF (tdist) THEN
READ (nin,*) theta(l)
l = l + 1
END IF
! mean
IF (mn==1) THEN
READ (nin,*) theta(l)
l = l + 1
END IF
! Regression parameters and pre-observed conditional variance
IF ( .NOT. copts(2)) THEN
READ (nin,*) theta(l:(l+nreg-1))
READ (nin,*) hp
END IF
! Fit the GARCH model
ifail = 0
CALL g13fef(dist,yt,x,ldx,num,ip,iq,nreg,mn,npar,theta,se,sc,covr, &
ldcovr,hp,et,ht,lgf,copts,maxit,tol,work,lwork,ifail)
! Read in forecast horizon
READ (nin,*) nt
ALLOCATE (fht(nt))
! Extract the estimate of the asymmetry parameter from theta
gamma = theta(pgamma)
! Calculate the volatility forecast
ifail = 0
CALL g13fff(num,nt,ip,iq,theta,gamma,fht,ht,et,ifail)
! Output the results
WRITE (nout,*) ' Parameter Standard'
WRITE (nout,*) ' estimates errors '
! Output the coefficient alpha_0
WRITE (nout,99999) 'Alpha', 0, theta(1), se(1)
l = 2
! Output the coefficients alpha_i
IF (iq>0) THEN
WRITE (nout,99999) ('Alpha',i-1,theta(i),se(i),i=l,l+iq-1)
l = l + iq
END IF
WRITE (nout,*)
! Output the coefficients beta_j
IF (ip>0) THEN
WRITE (nout,99999) (' Beta',i-l+1,theta(i),se(i),i=l,l+ip-1)
l = l + ip
WRITE (nout,*)
END IF
! Output the estimated asymmetry parameter, gamma
WRITE (nout,99998) ' Gamma', theta(l), se(l)
WRITE (nout,*)
l = l + 1
! Output the estimated degrees of freedom, df
IF (dist=='T') THEN
WRITE (nout,99998) ' DF', theta(l), se(l)
WRITE (nout,*)
l = l + 1
END IF
! Output the estimated mean term, b_0
IF (mn==1) THEN
WRITE (nout,99999) ' B', 0, theta(l), se(l)
l = l + 1
END IF
! Output the estimated linear regression coefficients, b_i
IF (nreg>0) THEN
WRITE (nout,99999) (' B',i-l+1,theta(i),se(i),i=l,l+nreg-1)
END IF
WRITE (nout,*)
! Display the volatility forecast
WRITE (nout,*)
WRITE (nout,99997) 'Volatility forecast = ', fht(nt)
WRITE (nout,*)
99999 FORMAT (1X,A,I0,1X,2F16.2)
99998 FORMAT (1X,A,1X,2F16.2)
99997 FORMAT (1X,A,F12.2)
END PROGRAM g13fefe
