Keyword: 陰的常微分方程式, 微分代数方程式, ODE, DAE
概要
本サンプルは微分代数方程式(DAE)を用いた陰的常微分方程式(ODE)の解を求めるFortranによるサンプルプログラムです。 本サンプルの例1では以下に示される陰的形式で記述されるスティッフなRobertson問題を解いて結果を出力します。
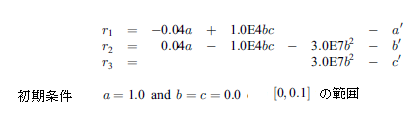
また例2では以下に示される代数方程式を解いて結果を出力します。
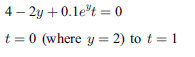
※本サンプルはnAG Fortranライブラリに含まれるルーチン d02nef() のExampleコードです。本サンプル及びルーチンの詳細情報は d02nef のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はd02nef のマニュアルページを参照)| このデータをダウンロード |
D02NEF Example Program Data 5 : ex1 : maxord 1 1 : ijac, itol 1.0E-3 1.0E-3 1.0E-3 : rtol 1.0E-6 1.0E-6 1.0E-6 : atol 0.0 0.0 0.0 : ydot 1.0 0.0 0.0 : y 0.0 0.0 : hmax, h0 0.0 0.02 : t, tout 5 : ex2 : maxord 1 1 : ijac, itol 0.0 : rtol 1.0E-8 : atol 0.0 : ydot 2.0 : y 0.0 0.0 : hmax, h0 0.0 0.2 : t, tout
- 1行目はタイトル行で読み飛ばされます。
- 2〜9行目は例1の入力データを指定しています。
- 2行目は後退微分公式(BDF)で使用される最大次数(maxord)を指定しています。
- 3行目はヤコビ行列の種類(ijac=1:解析的ヤコビ行列)と局所誤差のチェックの形式(itol=1:ベクトル)を指定しています。
- 4行目は相対局所誤差の許容値(rtol)を指定しています。
- 5行目は絶対局所誤差の許容値(atol)を指定しています。
- 6行目は時間導関数の近似値(ydot)を指定しています。
- 7行目は解の初期値(y)を指定しています。
- 8行目は最大絶対ステップサイズ(hmax:このオプションが不要の場合0.0を指定)と最初のステップのステップサイズ(h0:内部で計算される場合0.0を指定)を指定しています。
- 9行目は独立変数の初期値(t)と解が必要なtの次の値(tout)を指定しています。
- 11〜18行目は例2の入力データを指定しています。
出力結果
(本ルーチンの詳細はd02nef のマニュアルページを参照)| この出力例をダウンロード |
D02NEF Example Program Results
D02NEF Example 1
t Y(1) Y(2) Y(3)
0.0000 1.000000 0.000000 0.000000
0.0200 0.999204 0.000036 0.000760
0.0400 0.998415 0.000036 0.001549
0.0600 0.997631 0.000036 0.002333
0.0800 0.996852 0.000036 0.003112
0.1000 0.996080 0.000036 0.003884
The integrator completed task, ITASK = 3
D02NEF Example 2
t y(1)
0.0000 2.000000
0.2000 2.038016
0.4000 2.078379
0.6000 2.121462
0.8000 2.167736
1.0000 2.217821
The integrator completed task, ITASK = 3
- 5〜11行目には例1の独立変数の値と微分代数方程式の解が出力されています。
- 13行目に問題なく終了した積分により実行されたタスクが出力されています。"3"は解が要求される独立変数の値を超えて処理が進み積分が終了したことを意味します。
- 18〜24行目には例2の独立変数の値と微分代数方程式の解が出力されています。
- 26行目に問題なく終了した積分により実行されたタスクが出力されています。"3"は解が要求される独立変数の値を超えて処理が進み積分が終了したことを意味します。
ソースコード
(本ルーチンの詳細はd02nef のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
! D02NEF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
MODULE d02nefe_mod
! D02NEF Example Program Module:
! Parameters and User-defined Routines
! .. Use Statements ..
USE nag_library, ONLY : nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
REAL (KIND=nag_wp), PARAMETER :: alpha = 0.04_nag_wp
REAL (KIND=nag_wp), PARAMETER :: beta = 1.0E4_nag_wp
REAL (KIND=nag_wp), PARAMETER :: gamma = 3.0E7_nag_wp
REAL (KIND=nag_wp), PARAMETER :: one = 1.0_nag_wp
REAL (KIND=nag_wp), PARAMETER :: two = 2.0_nag_wp
INTEGER, PARAMETER :: ml = 1, mu = 2, neq1 = 3, &
neq2 = 1, nin = 5, nout = 6
CONTAINS
SUBROUTINE myjac1(neq,ml,mu,t,y,ydot,pd,cj)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: cj, t
INTEGER, INTENT (IN) :: ml, mu, neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: pd(2*ml+mu+1,neq)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
! .. Local Scalars ..
INTEGER :: md, ms
! .. Executable Statements ..
! Main diagonal pdfull(i,i), i=1,neq
md = mu + ml + 1
pd(md,1) = -alpha - cj
pd(md,2) = -beta*y(3) - two*gamma*y(2) - cj
pd(md,3) = -cj
! 1 Sub-diagonal pdfull(i+1:i), i=1,neq-1
ms = md + 1
pd(ms,1) = alpha
pd(ms,2) = two*gamma*y(2)
! First super-diagonal pdfull(i-1,i), i=2, neq
ms = md - 1
pd(ms,2) = beta*y(3)
pd(ms,3) = -beta*y(2)
! Second super-diagonal pdfull(i-2,i), i=3, neq
ms = md - 2
pd(ms,3) = beta*y(2)
RETURN
END SUBROUTINE myjac1
SUBROUTINE myjac2(neq,t,y,ydot,pd,cj)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: cj, t
INTEGER, INTENT (IN) :: neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: pd(neq*neq)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
! .. Intrinsic Functions ..
INTRINSIC exp
! .. Executable Statements ..
pd(1) = -two*y(1) + 0.1E0_nag_wp*t*y(1)*exp(y(1))
RETURN
END SUBROUTINE myjac2
SUBROUTINE res1(neq,t,y,ydot,r,ires,iuser,ruser)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: t
INTEGER, INTENT (INOUT) :: ires
INTEGER, INTENT (IN) :: neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: r(neq)
REAL (KIND=nag_wp), INTENT (INOUT) :: ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
INTEGER, INTENT (INOUT) :: iuser(*)
! .. Executable Statements ..
r(1) = -alpha*y(1) + beta*y(2)*y(3) - ydot(1)
r(2) = alpha*y(1) - beta*y(2)*y(3) - gamma*y(2)*y(2) - ydot(2)
r(3) = gamma*y(2)*y(2) - ydot(3)
RETURN
END SUBROUTINE res1
SUBROUTINE jac1(neq,t,y,ydot,pd,cj,iuser,ruser)
! .. Use Statements ..
USE nag_library, ONLY : d02nez
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: cj, t
INTEGER, INTENT (IN) :: neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (INOUT) :: pd(*), ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
INTEGER, INTENT (INOUT) :: iuser(*)
! .. Local Scalars ..
INTEGER :: ijac, ml, mu
! .. Executable Statements ..
ml = iuser(1)
mu = iuser(2)
ijac = iuser(3)
IF (ijac==1) THEN
CALL myjac1(neq,ml,mu,t,y,ydot,pd,cj)
ELSE
CALL d02nez(neq,t,y,ydot,pd,cj,iuser,ruser)
END IF
RETURN
END SUBROUTINE jac1
SUBROUTINE res2(neq,t,y,ydot,r,ires,iuser,ruser)
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: t
INTEGER, INTENT (INOUT) :: ires
INTEGER, INTENT (IN) :: neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: r(neq)
REAL (KIND=nag_wp), INTENT (INOUT) :: ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
INTEGER, INTENT (INOUT) :: iuser(*)
! .. Intrinsic Functions ..
INTRINSIC exp
! .. Executable Statements ..
r(1) = 4.0_nag_wp - y(1)**2 + t*0.1E0_nag_wp*exp(y(1))
RETURN
END SUBROUTINE res2
SUBROUTINE jac2(neq,t,y,ydot,pd,cj,iuser,ruser)
! .. Use Statements ..
USE nag_library, ONLY : d02nez
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (IN) :: cj, t
INTEGER, INTENT (IN) :: neq
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (INOUT) :: pd(*), ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: y(neq), ydot(neq)
INTEGER, INTENT (INOUT) :: iuser(*)
! .. Local Scalars ..
INTEGER :: ijac
! .. Executable Statements ..
ijac = iuser(1)
IF (ijac==1) THEN
CALL myjac2(neq,t,y,ydot,pd,cj)
ELSE
CALL d02nez(neq,t,y,ydot,pd,cj,iuser,ruser)
END IF
RETURN
END SUBROUTINE jac2
END MODULE d02nefe_mod
PROGRAM d02nefe
! D02NEF Example Main Program
! .. Use Statements ..
USE d02nefe_mod, ONLY : nout
! .. Implicit None Statement ..
IMPLICIT NONE
! .. External Subroutines ..
EXTERNAL ex1, ex2
! .. Executable Statements ..
WRITE (nout,*) 'D02NEF Example Program Results'
CALL ex1
CALL ex2
END PROGRAM d02nefe
SUBROUTINE ex1
! .. Use Statements ..
USE nag_library, ONLY : d02mcf, d02mwf, d02nef, d02npf, nag_wp
USE d02nefe_mod, ONLY : jac1, ml, mu, neq1, nin, nout, res1
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
REAL (KIND=nag_wp) :: h0, hmax, t, tout
INTEGER :: i, ifail, ijac, itask, itol, j, &
lcom, licom, maxord, neq
CHARACTER (8) :: jceval
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: atol(:), com(:), rtol(:), y(:), &
ydot(:)
REAL (KIND=nag_wp) :: ruser(1)
INTEGER, ALLOCATABLE :: icom(:)
INTEGER :: iuser(3)
! .. Executable Statements ..
WRITE (nout,*)
WRITE (nout,*) 'D02NEF Example 1'
! Skip heading in data file
READ (nin,*)
READ (nin,*) maxord
neq = neq1
lcom = 40 + (maxord+4)*neq + (2*ml+mu+1)*neq + 2*(neq/(ml+mu+1)+1)
licom = 50 + neq
ALLOCATE (atol(neq),com(lcom),rtol(neq),y(neq),ydot(neq),icom(licom))
READ (nin,*) ijac, itol
READ (nin,*) rtol(1:neq)
READ (nin,*) atol(1:neq)
READ (nin,*) ydot(1:neq)
IF (ijac==1) THEN
jceval = 'Analytic'
ELSE
jceval = 'Numeric'
END IF
! Set initial values
READ (nin,*) y(1:neq)
! Initialize the problem, specifying that the Jacobian is to be
! evaluated analytically using the provided routine jac.
READ (nin,*) hmax, h0
READ (nin,*) t, tout
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
CALL d02mwf(neq,maxord,jceval,hmax,h0,itol,icom,licom,com,lcom,ifail)
! Specify that the Jacobian is banded.
ifail = 0
CALL d02npf(neq,ml,mu,icom,licom,ifail)
! Use the iuser array to pass the band dimensions through to jac.
! An alternative would be to hard code values for ml and mu in jac.
iuser(1) = ml
iuser(2) = mu
iuser(3) = ijac
WRITE (nout,99999) (i,i=1,neq)
WRITE (nout,99998) t, (y(i),i=1,neq)
itask = 0
! Obtain the solution at 5 equally spaced values of T.
LOOP: DO j = 1, 5
ifail = -1
CALL d02nef(neq,t,tout,y,ydot,rtol,atol,itask,res1,jac1,icom,com, &
lcom,iuser,ruser,ifail)
WRITE (nout,99998) t, (y(i),i=1,neq)
IF (ifail/=0) THEN
WRITE (nout,99997) ifail
EXIT LOOP
END IF
tout = tout + 0.02_nag_wp
CALL d02mcf(icom)
END DO LOOP
WRITE (nout,*)
WRITE (nout,99996) itask
99999 FORMAT (/1X,' t ',5X,3(' Y(',I1,') '))
99998 FORMAT (1X,F8.4,3X,3(F12.6))
99997 FORMAT (1X,' ** D02NEF returned with IFAIL = ',I5)
99996 FORMAT (1X,'The integrator completed task, ITASK = ',I4)
END SUBROUTINE ex1
SUBROUTINE ex2
! .. Use Statements ..
USE nag_library, ONLY : d02mcf, d02mwf, d02nef, nag_wp
USE d02nefe_mod, ONLY : jac2, neq2, nin, nout, res2
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Local Scalars ..
REAL (KIND=nag_wp) :: h0, hmax, t, tout
INTEGER :: i, ifail, ijac, itask, itol, j, &
lcom, licom, maxord, neq
CHARACTER (8) :: jceval
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: atol(:), com(:), rtol(:), y(:), &
ydot(:)
REAL (KIND=nag_wp) :: ruser(1)
INTEGER, ALLOCATABLE :: icom(:)
INTEGER :: iuser(1)
! .. Executable Statements ..
WRITE (nout,*)
WRITE (nout,*) 'D02NEF Example 2'
WRITE (nout,*)
READ (nin,*)
READ (nin,*) maxord
neq = neq2
lcom = 40 + (maxord+4)*neq + neq*neq
licom = 50 + neq
ALLOCATE (atol(neq),com(lcom),rtol(neq),y(neq),ydot(neq),icom(licom))
READ (nin,*) ijac, itol
READ (nin,*) rtol(1:neq)
READ (nin,*) atol(1:neq)
READ (nin,*) ydot(1:neq)
IF (ijac==1) THEN
jceval = 'Analytic'
ELSE
jceval = 'Numeric'
END IF
! Initialize the problem, specifying that the Jacobian is to be
! evaluated analytically using the provided routine jac.
READ (nin,*) y(1:neq)
READ (nin,*) hmax, h0
READ (nin,*) t, tout
ifail = 0
CALL d02mwf(neq,maxord,jceval,hmax,h0,itol,icom,licom,com,lcom,ifail)
! Use the iuser array to pass whether numerical or analytic Jacobian
! is to be used.
iuser(1) = ijac
WRITE (nout,99999) (i,i=1,neq)
WRITE (nout,99998) t, y(1:neq)
itask = 0
! Obtain the solution at 5 equally spaced values of t.
LOOP: DO j = 1, 5
ifail = -1
CALL d02nef(neq,t,tout,y,ydot,rtol,atol,itask,res2,jac2,icom,com, &
lcom,iuser,ruser,ifail)
WRITE (nout,99998) t, y(1:neq)
IF (ifail/=0) THEN
WRITE (nout,99997) ifail
EXIT LOOP
END IF
tout = tout + 0.2_nag_wp
CALL d02mcf(icom)
END DO LOOP
WRITE (nout,*)
WRITE (nout,99996) itask
99999 FORMAT (/1X,' t y(',I1,')')
99998 FORMAT (1X,F8.4,3X,3(F12.6))
99997 FORMAT (1X,' ** D02NEF returned with IFAIL = ',I5)
99996 FORMAT (1X,'The integrator completed task, ITASK = ',I4)
END SUBROUTINE ex2
