Keyword: カイ二乗適合度, chi-square, goodness of fit test, 検定
概要
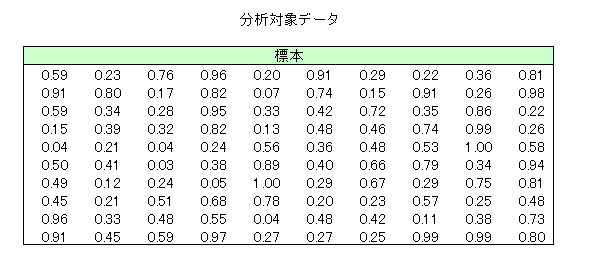
本サンプルはカイ二乗適合度検定(the chi-square goodness of fit test) を行うFortranによるサンプルプログラムです。 本サンプルは以下に示されるランダムな標本が特定の分布から生じているという帰無仮説を検定し、カイ二乗検定統計量、自由度、有意水準と検定統計量の寄与率を算出します。
※本サンプルはnAG Fortranライブラリに含まれるルーチン g08cgf() のExampleコードです。本サンプル及びルーチンの詳細情報は g08cgf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はg08cgf のマニュアルページを参照)| このデータをダウンロード |
G08CGF Example Program Data 100 :: N 5 1 :: NCLASS,ICLASS 0.59 0.23 0.76 0.96 0.20 0.91 0.29 0.22 0.36 0.81 0.91 0.80 0.17 0.82 0.07 0.74 0.15 0.91 0.26 0.98 0.59 0.34 0.28 0.95 0.33 0.42 0.72 0.35 0.86 0.22 0.15 0.39 0.32 0.82 0.13 0.48 0.46 0.74 0.99 0.26 0.04 0.21 0.04 0.24 0.56 0.36 0.48 0.53 1.00 0.58 0.50 0.41 0.03 0.38 0.89 0.40 0.66 0.79 0.34 0.94 0.49 0.12 0.24 0.05 1.00 0.29 0.67 0.29 0.75 0.81 0.45 0.21 0.51 0.68 0.78 0.20 0.23 0.57 0.25 0.48 0.96 0.33 0.48 0.55 0.04 0.48 0.42 0.11 0.38 0.73 0.91 0.45 0.59 0.97 0.27 0.27 0.25 0.99 0.99 0.80 :: End of X 0.2 0.4 0.6 0.8 :: CB 'U' 0 :: DIST,NPEST 0.0 1.0 :: PAR
- 1行目はタイトル行で読み飛ばされます。
- 2行目に観測値の数(n)を指定しています。
- 3行目に階級数(nclass=5)、階級の境界値が計算されるのかユーザによって提供されるのか(iclass=1)を指定しています。"1"はユーザによって階級の境界値が提供されることを意味しています。
- 4〜13行目に観測値(x)を指定しています。
- 14行目に階級の上限値(cb)を指定しています。
- 15行目に検定が実行される分布の種類(dist='U')と推定パラメータの数(npest=0)を指定しています。"U"は一様分布を意味しています。
- 16行目に一様分布の下限と上限(par)を指定しています。
出力結果
(本ルーチンの詳細はg08cgf のマニュアルページを参照)| この出力例をダウンロード |
G08CGF Example Program Results
Chi-squared test statistic = 14.2000
Degrees of freedom. = 4
Significance level = 0.0067
The contributions to the test statistic are :-
3.2000
6.0500
0.4500
4.0500
0.4500
- 3行目にはカイ二乗検定統計量が出力されています。
- 4行目には自由度が出力されています。
- 5行目には有意水準が出力されています。
- 8行目〜12行目には各階級の検定統計量への寄与率が出力されています。
ソースコード
(本ルーチンの詳細はg08cgf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM g08cgfe
! G08CGF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : g01aef, g08cgf, nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: chisq, p, xmax, xmin
INTEGER :: iclass, ifail, n, nclass, ndf, npar, &
npest
CHARACTER (1) :: dist
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: cb(:), chisqi(:), eval(:), prob(:), &
x(:)
REAL (KIND=nag_wp) :: par(2)
INTEGER, ALLOCATABLE :: ifreq(:)
! .. Executable Statements ..
WRITE (nout,*) 'G08CGF Example Program Results'
WRITE (nout,*)
! Skip heading in data file
READ (nin,*)
! Read in problem size
READ (nin,*) n
! Read in class information
READ (nin,*) nclass, iclass
ALLOCATE (x(n),cb(nclass),ifreq(nclass),prob(nclass),eval(nclass), &
chisqi(nclass))
! Read in data
READ (nin,*) x(1:n)
! Read in the class boundaries, if supplied
IF (iclass==1) THEN
READ (nin,*) cb(1:(nclass-1))
END IF
! Read in information on the distribution to test against
READ (nin,*) dist, npest
SELECT CASE (dist)
CASE ('A','a')
npar = 0
CASE ('E','e','C','c')
npar = 1
CASE DEFAULT
npar = 2
END SELECT
! Read in the distribution parameters or probabilities
IF (npar==0) THEN
READ (nin,*) prob(1:nclass)
ELSE
READ (nin,*) par(1:npar)
END IF
! Produce frequency table for data
ifail = 0
CALL g01aef(n,nclass,x,iclass,cb,ifreq,xmin,xmax,ifail)
! Perform chi-squared test
ifail = -1
CALL g08cgf(nclass,ifreq,cb,dist,par,npest,prob,chisq,p,ndf,eval, &
chisqi,ifail)
IF (ifail/=0) THEN
IF (ifail<=9) THEN
GO TO 20
END IF
END IF
! Display results
WRITE (nout,99999) 'Chi-squared test statistic = ', chisq
WRITE (nout,99998) 'Degrees of freedom. = ', ndf
WRITE (nout,99999) 'Significance level = ', p
WRITE (nout,*)
WRITE (nout,*) 'The contributions to the test statistic are :-'
WRITE (nout,99997) chisqi(1:nclass)
20 CONTINUE
99999 FORMAT (1X,A,F10.4)
99998 FORMAT (1X,A,I5)
99997 FORMAT (1X,F10.4)
END PROGRAM g08cgfe
