Keyword: ブラック・ショールズ・マートン, オプション, プライシング
概要
本サンプルはブラック・ショールズ・マートンオプションプライシングを求めるFortranによるサンプルプログラムです。 本サンプルは以下に示されるブラック・ショールズ・マートンの公式を用いてオプションプライシングを求めて出力します。
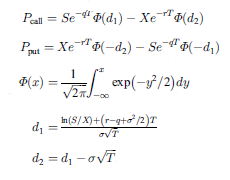
※本サンプルはnAG Fortranライブラリに含まれるルーチン s30aaf() のExampleコードです。本サンプル及びルーチンの詳細情報は s30aaf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本ルーチンの詳細はs30aaf のマニュアルページを参照)| このデータをダウンロード |
S30AAF Example Program Data 'C' : Call = 'C', Put = 'P' 55.0 0.3 0.1 0.0 : S, SIGMA, R, Q 3 2 : M, N 58.0 60.0 62.0 : X(I), I = 1,2,...M 0.7 0.8 : T(I), I = 1,2,...N
- 1行目はタイトル行で読み飛ばされます。
- 2行目にオプションがコール(='C':買い)かプット(='P':売り)か(calput)を指定しています。
- 3行目に原資産価格(s=55.0)、原資産のボラティリティ(sigma=0.3)、無リスク利子率(r=0.1)、配当利回り(q=0.0)を指定しています。
- 4行目に行使価格の数(m=3)、満期までの期間の数(n=2)を指定しています。
- 5〜7行目に行使価格(x)を指定しています。
- 8〜9行目に満期までの期間(t)を指定しています。
出力結果
(本ルーチンの詳細はs30aaf のマニュアルページを参照)| この出力例をダウンロード |
S30AAF Example Program Results
Black-Scholes-Merton formula
European Call :
Spot = 55.0000
Volatility = 0.3000
Rate = 0.1000
Dividend = 0.0000
Strike Expiry Option Price
58.0000 0.7000 5.9198
58.0000 0.8000 6.5506
60.0000 0.7000 5.0809
60.0000 0.8000 5.6992
62.0000 0.7000 4.3389
62.0000 0.8000 4.9379
- 5行目に原資産価格が出力されています。
- 6行目に原資産のボラティリティが出力されています。
- 7行目に無リスク利子率が出力されています。
- 8行目に配当利回りが出力されています。
- 10〜16行目に行使価格、満期までの期間、オプション価格が出力されています。
ソースコード
(本ルーチンの詳細はs30aaf のマニュアルページを参照)
※本サンプルソースコードは科学技術・統計計算ライブラリである「nAG Fortranライブラリ」のルーチンを呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
PROGRAM s30aafe
! S30AAF Example Program Text
! Mark 23 Release. nAG Copyright 2011.
! .. Use Statements ..
USE nag_library, ONLY : nag_wp, s30aaf
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
INTEGER, PARAMETER :: nin = 5, nout = 6
! .. Local Scalars ..
REAL (KIND=nag_wp) :: q, r, s, sigma
INTEGER :: i, ifail, j, ldp, m, n
CHARACTER (1) :: calput
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: p(:,:), t(:), x(:)
! .. Executable Statements ..
WRITE (nout,*) 'S30AAF Example Program Results'
! Skip heading in data file
READ (nin,*)
READ (nin,*) calput
READ (nin,*) s, sigma, r, q
READ (nin,*) m, n
ldp = m
ALLOCATE (p(ldp,n),t(n),x(m))
READ (nin,*) (x(i),i=1,m)
READ (nin,*) (t(i),i=1,n)
ifail = 0
CALL s30aaf(calput,m,n,x,s,t,sigma,r,q,p,ldp,ifail)
WRITE (nout,*)
WRITE (nout,*) 'Black-Scholes-Merton formula'
SELECT CASE (calput)
CASE ('C','c')
WRITE (nout,*) 'European Call :'
CASE ('P','p')
WRITE (nout,*) 'European Put :'
END SELECT
WRITE (nout,99998) ' Spot = ', s
WRITE (nout,99998) ' Volatility = ', sigma
WRITE (nout,99998) ' Rate = ', r
WRITE (nout,99998) ' Dividend = ', q
WRITE (nout,*)
WRITE (nout,*) ' Strike Expiry Option Price'
DO i = 1, m
DO j = 1, n
WRITE (nout,99999) x(i), t(j), p(i,j)
END DO
END DO
99999 FORMAT (1X,2(F9.4,1X),6X,F9.4)
99998 FORMAT (A,1X,F8.4)
END PROGRAM s30aafe
