Keyword: 実一般行列, 特異値主要項
概要
本サンプルは実一般行列の特異値主要項を求めるC言語によるサンプルプログラムです。 本サンプルは2次元カーネルが以下の式で示される場合の有限差分の離散化から得られる100x500の実行列の最大特異値4つを求めて出力します。
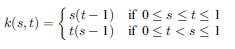
※本サンプルはnAG Cライブラリに含まれる関数 nag_real_partial_svd() のExampleコードです。本サンプル及び関数の詳細情報は nag_real_partial_svd のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_real_partial_svd のマニュアルページを参照)| このデータをダウンロード |
nag_real_partial_svd (f02wgc) Example Program Data 100 500 4 10 : Values for m n nev and ncv
- 1行目はタイトル行で読み飛ばされます。
- 2行目に行列Aの行数(m)、列数(n)、特異値の数(nev)、特異値と残差の配列の次数(ncv)を指定しています。
出力結果
(本関数の詳細はnag_real_partial_svd のマニュアルページを参照)| この出力例をダウンロード |
nag_real_partial_svd (f02wgc) Example Program Results (User-supplied callback av, first invocation.) Singular Value Residual 0.00830 3.6e-18 0.01223 8.2e-18 0.02381 4.7e-18 0.11274 2.5e-17
- 4〜7行目に特異値と残差が出力されています。
ソースコード
(本関数の詳細はnag_real_partial_svd のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_real_partial_svd (f02wgc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
/* Pre-processor includes */
#include <stdio.h>
#include <math.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagf02.h>
#ifdef __cplusplus
extern "C"
{
#endif
static void nAG_CALL av(Integer *iflag, Integer m, Integer n,
const double x[], double ax[], Nag_Comm *comm);
#ifdef __cplusplus
}
#endif
int main(void)
{
/*Integer scalar and array declarations */
Integer exit_status = 0;
Integer i, m, n, nconv, ncv, nev;
Integer pdu, pdv;
Nag_Comm comm;
NagError fail;
/*Double scalar and array declarations */
static double ruser[1] = { -1.0 };
double *resid = 0, *sigma = 0, *u = 0, *v = 0;
Nag_OrderType order;
INIT_FAIL(fail);
printf("nag_real_partial_svd (f02wgc) Example Program Results\n\n");
/* For communication with user-supplied functions: */
comm.user = ruser;
/* Skip heading in data file */
scanf("%*[^\n] ");
scanf("%ld%ld%ld%ld%*[^\n]", &m, &n,
&nev, &ncv);
#ifdef nAG_COLUMN_MAJOR
order = Nag_ColMajor;
pdu = m;
pdv = n;
#else
order = Nag_RowMajor;
pdu = ncv;
pdv = ncv;
#endif
if (!(resid = nAG_ALLOC(m, double)) ||
!(sigma = nAG_ALLOC(ncv, double)) ||
!(u = nAG_ALLOC(m * ncv, double)) || !(v = nAG_ALLOC(n * ncv, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
/*
* nag_real_partial_svd (f02wgc)
* Computes leading terms in the singular value decomposition of
* a real general matrix; also computes corresponding left and right
* singular vectors.
*/
nag_real_partial_svd(order, m, n, nev, ncv, av, &nconv, sigma, u, pdu,
v, pdv, resid, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_real_partial_svd (f02wgc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Print computed residuals */
printf("%s\n", " Singular Value Residual");
for (i = 0; i < nconv; i++)
printf("%10.5f %16.2g\n", sigma[i], resid[i]);
printf("\n");
END:
nAG_FREE(resid);
nAG_FREE(sigma);
nAG_FREE(u);
nAG_FREE(v);
return exit_status;
}
static void nAG_CALL av(Integer *iflag, Integer m, Integer n,
const double x[], double ax[], Nag_Comm *comm)
{
Integer i, j;
double one = 1.0, zero = 0.0;
double h, k, s, t;
/* Matrix vector multiply: w <- A*x or w <- Trans(A)*x. */
if (comm->user[0] == -1.0) {
printf("(User-supplied callback av, first invocation.)\n");
comm->user[0] = 0.0;
}
h = one / (double) (m + 1);
k = one / (double) (n + 1);
if (*iflag == 1) {
for (i = 0; i < m; i++)
ax[i] = zero;
t = zero;
for (j = 0; j < n; j++) {
t = t + k;
s = zero;
for (i = 0; i < MIN(j + 1, m); i++) {
s = s + h;
ax[i] = ax[i] + k * s * (t - one) * x[j];
}
for (i = j + 1; i < m; i++) {
s = s + h;
ax[i] = ax[i] + k * t * (s - one) * x[j];
}
}
}
else {
for (i = 0; i < n; i++)
ax[i] = zero;
t = zero;
for (j = 0; j < n; j++) {
t = t + k;
s = zero;
for (i = 0; i < MIN(j + 1, m); i++) {
s = s + h;
ax[j] = ax[j] + k * s * (t - one) * x[i];
}
for (i = j + 1; i < m; i++) {
s = s + h;
ax[j] = ax[j] + k * t * (s - one) * x[i];
}
}
}
return;
}
