Keyword: チェビシェフ, 選点法, 放物型偏微分方程式
概要
本サンプルはチェビシェフC0選点法を用いた離散化により放物型偏微分方程式を解くC言語によるサンプルプログラムです。 本サンプルは以下に示される1組の2次の放物型偏微分方程式(PDE)で記述される4次の偏微分方程式(PDE)を解いて結果を出力します。
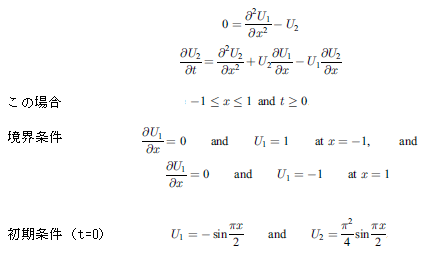
※本サンプルはnAG Cライブラリに含まれる関数 nag_pde_parab_1d_coll() のExampleコードです。本サンプル及び関数の詳細情報は nag_pde_parab_1d_coll のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
出力結果
(本関数の詳細はnag_pde_parab_1d_coll のマニュアルページを参照)| この出力例をダウンロード |
nag_pde_parab_1d_coll (d03pdc) Example Program Results
Polynomial degree = 3 No. of elements = 9
Accuracy requirement = 1.000e-04 Number of points = 28
t / x -1.0000 -0.6000 -0.2000 0.2000 0.6000 1.0000
(User-supplied callback uinit, first invocation.)
(User-supplied callback pdedef, first invocation.)
(User-supplied callback bndary, first invocation.)
0.0001 u(1) 1.0000 0.8090 0.3090 -0.3090 -0.8090 -1.0000
u(2) -2.4850 -1.9957 -0.7623 0.7623 1.9957 2.4850
0.0010 u(1) 1.0000 0.8085 0.3088 -0.3088 -0.8085 -1.0000
u(2) -2.5583 -1.9913 -0.7606 0.7606 1.9913 2.5583
0.0100 u(1) 1.0000 0.8051 0.3068 -0.3068 -0.8051 -1.0000
u(2) -2.6962 -1.9481 -0.7439 0.7439 1.9481 2.6962
0.1000 u(1) 1.0000 0.7951 0.2985 -0.2985 -0.7951 -1.0000
u(2) -2.9022 -1.8339 -0.6338 0.6338 1.8339 2.9022
1.0000 u(1) 1.0000 0.7939 0.2972 -0.2972 -0.7939 -1.0000
u(2) -2.9233 -1.8247 -0.6120 0.6120 1.8247 2.9233
Number of integration steps in time 50
Number of residual evaluations of resulting ODE system 407
Number of Jacobian evaluations 18
Number of iterations of nonlinear solver 122
- 3行目にはチェビシェフ多項式の次数と要素の数が出力されています。
- 5行目には誤差推定を制御するための正数とメッシュ点の数が出力されています。
- 7行目にはブレークポイントが出力されています。
- 10〜23行目には独立変数の値とU1(x,t)とU2(x,t)の計算結果が出力されています。
- 25行目には積分のステップの数が出力されています。
- 26行目には結果として生じる常微分方程式(ODE)の残差評価の数が出力されています。
- 27行目にはヤコビアン評価の数が出力されています。
- 28行目には非線形ソルバの反復数が出力されています。
ソースコード
(本関数の詳細はnag_pde_parab_1d_coll のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_pde_parab_1d_coll (d03pdc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <stdio.h>
#include <math.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagd03.h>
#include <nagx01.h>
#ifdef __cplusplus
extern "C"
{
#endif
static void nAG_CALL uinit(Integer, Integer, const double[], double[],
Nag_Comm *);
static void nAG_CALL pdedef(Integer, double, const double[], Integer,
const double[], const double[], double[],
double[], double[], Integer *, Nag_Comm *);
static void nAG_CALL bndary(Integer, double, const double[], const double[],
Integer, double[], double[], Integer *,
Nag_Comm *);
#ifdef __cplusplus
}
#endif
#define U(I, J) u[npde*((J) -1)+(I) -1]
#define UOUT(I, J, K) uout[npde*(intpts*((K) -1)+(J) -1)+(I) -1]
#define P(I, J, K) p[npde*(npde*((K) -1)+(J) -1)+(I) -1]
#define Q(I, J) q[npde*((J) -1)+(I) -1]
#define R(I, J) r[npde*((J) -1)+(I) -1]
#define UX(I, J) ux[npde*((J) -1)+(I) -1]
int main(void)
{
const Integer nbkpts = 10, nelts = nbkpts - 1, npde = 2, npoly = 3,
m = 0, itype = 1, npts = nelts * npoly + 1, neqn = npde * npts,
intpts = 6, npl1 = npoly + 1, lisave = neqn + 24,
mu = npde * (npoly + 1) - 1, lenode = (3 * mu + 1) * neqn,
nwkres =
3 * npl1 * npl1 + npl1 * (npde * npde + 6 * npde + nbkpts + 1)
+ 13 * npde + 5, lrsave = 11 * neqn + 50 + nwkres + lenode;
static double ruser[3] = { -1.0, -1.0, -1.0 };
static double xout[6] = { -1., -.6, -.2, .2, .6, 1. };
double acc, tout, ts;
Integer exit_status = 0, i, ind, it, itask, itrace;
double *rsave = 0, *u = 0, *uout = 0, *x = 0, *xbkpts = 0;
Integer *isave = 0;
NagError fail;
Nag_Comm comm;
Nag_D03_Save saved;
INIT_FAIL(fail);
printf("nag_pde_parab_1d_coll (d03pdc) Example Program Results\n\n");
/* For communication with user-supplied functions: */
comm.user = ruser;
/* Allocate memory */
if (!(rsave = nAG_ALLOC(lrsave, double)) ||
!(u = nAG_ALLOC(npde * npts, double)) ||
!(uout = nAG_ALLOC(npde * intpts * itype, double)) ||
!(x = nAG_ALLOC(npts, double)) ||
!(xbkpts = nAG_ALLOC(nbkpts, double)) ||
!(isave = nAG_ALLOC(lisave, Integer)))
{
printf("Allocation failure\n");
exit_status = 1;
goto END;
}
acc = 1e-4;
itrace = 0;
/* Set the break-points */
for (i = 0; i < 10; ++i) {
xbkpts[i] = i * 2.0 / 9.0 - 1.0;
}
ind = 0;
itask = 1;
ts = 0.0;
tout = 1e-5;
printf(" Polynomial degree =%4ld", npoly);
printf(" No. of elements = %4ld\n\n", nelts);
printf(" Accuracy requirement = %12.3e", acc);
printf(" Number of points = %5ld\n\n", npts);
printf(" t / x ");
for (i = 0; i < 6; ++i) {
printf("%8.4f", xout[i]);
printf((i + 1) % 6 == 0 || i == 5 ? "\n" : "");
}
printf("\n");
/* Loop over output values of t */
for (it = 0; it < 5; ++it) {
tout *= 10.0;
/* nag_pde_parab_1d_coll (d03pdc).
* General system of parabolic PDEs, method of lines,
* Chebyshev C^0 collocation, one space variable
*/
nag_pde_parab_1d_coll(npde, m, &ts, tout, pdedef, bndary, u, nbkpts,
xbkpts, npoly, npts, x, uinit, acc, rsave, lrsave,
isave, lisave, itask, itrace, 0, &ind, &comm,
&saved, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_pde_parab_1d_coll (d03pdc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
/* Interpolate at required spatial points */
/* nag_pde_interp_1d_coll (d03pyc).
* PDEs, spatial interpolation with nag_pde_parab_1d_coll
* (d03pdc) or nag_pde_parab_1d_coll_ode (d03pjc)
*/
nag_pde_interp_1d_coll(npde, u, nbkpts, xbkpts, npoly, npts, xout,
intpts, itype, uout, rsave, lrsave, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_pde_interp_1d_coll (d03pyc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
printf("\n %6.4f u(1)", tout);
for (i = 1; i <= 6; ++i) {
printf("%8.4f", UOUT(1, i, 1));
printf(i % 6 == 0 || i == 6 ? "\n" : "");
}
printf(" u(2)");
for (i = 1; i <= 6; ++i) {
printf("%8.4f", UOUT(2, i, 1));
printf(i % 6 == 0 || i == 6 ? "\n" : "");
}
}
/* Print integration statistics */
printf("\n");
printf(" Number of integration steps in time ");
printf("%4ld\n", isave[0]);
printf(" Number of residual evaluations of resulting ODE system ");
printf("%4ld\n", isave[1]);
printf(" Number of Jacobian evaluations ");
printf("%4ld\n", isave[2]);
printf(" Number of iterations of nonlinear solver ");
printf("%4ld\n", isave[4]);
END:
nAG_FREE(rsave);
nAG_FREE(u);
nAG_FREE(uout);
nAG_FREE(x);
nAG_FREE(xbkpts);
nAG_FREE(isave);
return exit_status;
}
static void nAG_CALL uinit(Integer npde, Integer npts, const double x[],
double u[], Nag_Comm *comm)
{
Integer i;
double piby2;
if (comm->user[0] == -1.0) {
printf("(User-supplied callback uinit, first invocation.)\n");
comm->user[0] = 0.0;
}
piby2 = 0.5 * nag_pi;
for (i = 1; i <= npts; ++i) {
U(1, i) = -sin(piby2 * x[i - 1]);
U(2, i) = -piby2 * piby2 * U(1, i);
}
return;
}
static void nAG_CALL pdedef(Integer npde, double t, const double x[],
Integer nptl, const double u[], const double ux[],
double p[], double q[], double r[], Integer *ires,
Nag_Comm *comm)
{
Integer i;
if (comm->user[1] == -1.0) {
printf("(User-supplied callback pdedef, first invocation.)\n");
comm->user[1] = 0.0;
}
for (i = 1; i <= nptl; ++i) {
Q(1, i) = U(2, i);
Q(2, i) = U(1, i) * UX(2, i) - UX(1, i) * U(2, i);
R(1, i) = UX(1, i);
R(2, i) = UX(2, i);
P(1, 1, i) = 0.0;
P(1, 2, i) = 0.0;
P(2, 1, i) = 0.0;
P(2, 2, i) = 1.0;
}
return;
}
static void nAG_CALL bndary(Integer npde, double t, const double u[],
const double ux[], Integer ibnd, double beta[],
double gamma[], Integer *ires, Nag_Comm *comm)
{
if (comm->user[2] == -1.0) {
printf("(User-supplied callback bndary, first invocation.)\n");
comm->user[2] = 0.0;
}
if (ibnd == 0) {
beta[0] = 1.0;
gamma[0] = 0.0;
beta[1] = 0.0;
gamma[1] = u[0] - 1.0;
}
else {
beta[0] = 1.0;
gamma[0] = 0.0;
beta[1] = 0.0;
gamma[1] = u[0] + 1.0;
}
return;
}
