Keyword: 後退差分公式, 常微分方程式
概要
本サンプルは後退差分公式を用いた常微分方程式を求めるC言語によるサンプルプログラムです。 本サンプルは以下に示される常微分方程式について5つのケースの計算をし、出力します。
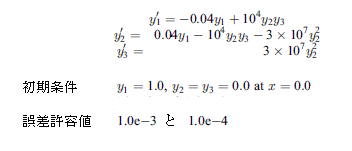
※本サンプルはnAG Cライブラリに含まれる関数 nag_ode_ivp_bdf_gen() のExampleコードです。本サンプル及び関数の詳細情報は nag_ode_ivp_bdf_gen のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
出力結果
(本関数の詳細はnag_ode_ivp_bdf_gen のマニュアルページを参照)| この出力例をダウンロード |
nag_ode_ivp_bdf_gen (d02ejc) Example Program Results
Case 1: calculating Jacobian internally
intermediate output, root-finding
Calculation with tol = 1.0e-03
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
(User-supplied callback g, first invocation.)
(User-supplied callback fcn, first invocation.)
2.00 0.9416 0.00003 0.0583
4.00 0.9055 0.00002 0.0945
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Calculation with tol = 1.0e-04
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
2.00 0.9416 0.00003 0.0584
4.00 0.9055 0.00002 0.0945
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Case 2: calculating Jacobian by pederv
intermediate output, root-finding
Calculation with tol = 1.0e-03
X Y(1) Y(2) Y(3)
(User-supplied callback pederv, first invocation.)
0.00 1.0000 0.00000 0.0000
2.00 0.9416 0.00003 0.0583
4.00 0.9055 0.00002 0.0945
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Calculation with tol = 1.0e-04
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
2.00 0.9416 0.00003 0.0584
4.00 0.9055 0.00002 0.0945
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Case 3: calculating Jacobian internally
no intermediate output, root-finding
Calculation with tol = 1.0e-03
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Calculation with tol = 1.0e-04
Root of Y(1)-0.9 at 4.377
Solution is 0.9000 0.00002 0.1000
Case 4: calculating Jacobian internally
intermediate output, no root-finding
Calculation with tol = 1.0e-03
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
2.00 0.9416 0.00003 0.0583
4.00 0.9055 0.00002 0.0945
6.00 0.8793 0.00002 0.1207
8.00 0.8586 0.00002 0.1414
10.00 0.8414 0.00002 0.1586
10.00 0.8414 0.00002 0.1586
Calculation with tol = 1.0e-04
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
2.00 0.9416 0.00003 0.0584
4.00 0.9055 0.00002 0.0945
6.00 0.8793 0.00002 0.1207
8.00 0.8585 0.00002 0.1414
10.00 0.8414 0.00002 0.1586
10.00 0.8414 0.00002 0.1586
Case 5: calculating Jacobian internally
no intermediate output, no root-finding (integrate to xend)
Calculation with tol = 1.0e-03
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
10.00 0.8414 0.00002 0.1586
Calculation with tol = 1.0e-04
X Y(1) Y(2) Y(3)
0.00 1.0000 0.00000 0.0000
10.00 0.8414 0.00002 0.1586
- 3〜21行目にはケース1の結果が出力されています。ケース1ではy=0.9となるデータ点が見つかるまで 2.0の間隔でx=10.0まで計算を行い、中間結果を出力しています。ヤコビ行列を数値的に計算しています。
- 9〜11行目にxの値と許容値 1.0e-003 で計算したyの値が出力されています。
- 12行目にy=0.9となるデータ点が出力されています。
- 13行目に常微分方程式の解が出力されています。
- 15〜19行目にxの値と許容値 1.0e-004 で計算したyの値が出力されています。
- 20行目にy=0.9となるデータ点が出力されています。
- 21行目に常微分方程式の解が出力されています。
- 23〜41行目にはケース2の結果が出力されています。ケース2ではケース1と同様の計算を行い、中間結果を出力し解が見つかったら終了します。ヤコビ行列を分析的に計算しています。
- 43〜53行目にケース3の結果が出力されています。ケース3ではケース1と同様の計算を行いますが、中間結果の出力を行わず、解が見つかったら終了します。
- 55〜77行目にケース4の結果が出力されています。ケース4ではケース1と同様の計算を行いますが、中間結果を出力し、x=10.0まで計算を行っています。
- 79〜91行目にケース5の結果が出力されています。ケース5ではケース1と同様の計算を行いますが中間結果の出力を行わず、x=10.0まで計算を行っています。
ソースコード
(本関数の詳細はnag_ode_ivp_bdf_gen のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_ode_ivp_bdf_gen (d02ejc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
#include <nag.h>
#include <math.h>
#include <stdio.h>
#include <nag_stdlib.h>
#include <nagd02.h>
#ifdef __cplusplus
extern "C"
{
#endif
static void nAG_CALL fcn(Integer neq, double x, const double y[],
double f[], Nag_User *comm);
static void nAG_CALL pederv(Integer neq, double x, const double y[],
double pw[], Nag_User *comm);
static double nAG_CALL g(Integer neq, double x, const double y[],
Nag_User *comm);
static void nAG_CALL out(Integer neq, double *tsol, const double y[],
Nag_User *comm);
#ifdef __cplusplus
}
#endif
struct user
{
double xend, h;
Integer k;
Integer *use_comm;
};
#define NEQ 3
int main(void)
{
static Integer use_comm[4] = { 1, 1, 1, 1 };
Integer exit_status = 0, j, neq;
NagError fail;
Nag_User comm;
double tol, x, *y = 0;
struct user s;
INIT_FAIL(fail);
printf("nag_ode_ivp_bdf_gen (d02ejc) Example Program Results\n");
/* For communication with user-supplied functions
* assign address of user defined structure
* to comm.p.
*/
s.use_comm = use_comm;
comm.p = (Pointer) &s;
neq = NEQ;
if (neq >= 1) {
if (!(y = nAG_ALLOC(neq, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
}
else {
exit_status = 1;
return exit_status;
}
s.xend = 10.0;
printf("\nCase 1: calculating Jacobian internally\n");
printf(" intermediate output, root-finding\n\n");
for (j = 3; j <= 4; ++j) {
tol = pow(10.0, -(double) j);
printf("\n Calculation with tol = %10.1e\n", tol);
x = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
s.k = 4;
s.h = (s.xend - x) / (double) (s.k + 1);
printf(" X Y(1) Y(2) Y(3)\n");
/* nag_ode_ivp_bdf_gen (d02ejc).
* Ordinary differential equations solver, stiff, initial
* value problems using the Backward Differentiation
* Formulae
*/
nag_ode_ivp_bdf_gen(neq, fcn, NULLFN, &x, y, s.xend, tol, Nag_Relative,
out, g, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_ode_ivp_bdf_gen (d02ejc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf(" Root of Y(1)-0.9 at %5.3f\n", x);
printf(" Solution is ");
printf("%7.4f %8.5f %7.4f\n", y[0], y[1], y[2]);
}
printf("\nCase 2: calculating Jacobian by pederv\n");
printf(" intermediate output, root-finding\n\n");
for (j = 3; j <= 4; ++j) {
tol = pow(10.0, -(double) j);
printf("\n Calculation with tol = %10.1e\n", tol);
x = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
s.k = 4;
s.h = (s.xend - x) / (double) (s.k + 1);
printf(" X Y(1) Y(2) Y(3)\n");
/* nag_ode_ivp_bdf_gen (d02ejc), see above. */
nag_ode_ivp_bdf_gen(neq, fcn, pederv, &x, y, s.xend, tol, Nag_Relative,
out, g, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_ode_ivp_bdf_gen (d02ejc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf(" Root of Y(1)-0.9 at %5.3f\n", x);
printf(" Solution is ");
printf("%7.4f %8.5f %7.4f\n", y[0], y[1], y[2]);
}
printf("\nCase 3: calculating Jacobian internally\n");
printf(" no intermediate output, root-finding\n\n");
for (j = 3; j <= 4; ++j) {
tol = pow(10.0, -(double) j);
printf("\n Calculation with tol = %10.1e\n", tol);
x = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
/* nag_ode_ivp_bdf_gen (d02ejc), see above. */
nag_ode_ivp_bdf_gen(neq, fcn, NULLFN, &x, y, s.xend, tol, Nag_Relative,
NULLFN, g, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_ode_ivp_bdf_gen (d02ejc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf(" Root of Y(1)-0.9 at %5.3f\n", x);
printf(" Solution is ");
printf("%7.4f %8.5f %7.4f\n", y[0], y[1], y[2]);
}
printf("\nCase 4: calculating Jacobian internally\n");
printf(" intermediate output, no root-finding\n\n");
for (j = 3; j <= 4; ++j) {
tol = pow(10.0, -(double) j);
printf("\n Calculation with tol = %10.1e\n", tol);
x = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
s.k = 4;
s.h = (s.xend - x) / (double) (s.k + 1);
printf(" X Y(1) Y(2) Y(3)\n");
/* nag_ode_ivp_bdf_gen (d02ejc), see above. */
nag_ode_ivp_bdf_gen(neq, fcn, NULLFN, &x, y, s.xend, tol, Nag_Relative,
out, NULLDFN, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_ode_ivp_bdf_gen (d02ejc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf("%8.2f", x);
printf("%13.4f%13.5f%13.4f\n", y[0], y[1], y[2]);
}
printf("\nCase 5: calculating Jacobian internally\n");
printf(" no intermediate output, no root-finding (integrate to xend)\n\n");
for (j = 3; j <= 4; ++j) {
tol = pow(10.0, -(double) j);
printf("\n Calculation with tol = %10.1e\n", tol);
x = 0.0;
y[0] = 1.0;
y[1] = 0.0;
y[2] = 0.0;
printf(" X Y(1) Y(2) Y(3)\n");
printf("%8.2f", x);
printf("%13.4f%13.5f%13.4f\n", y[0], y[1], y[2]);
/* nag_ode_ivp_bdf_gen (d02ejc), see above. */
nag_ode_ivp_bdf_gen(neq, fcn, NULLFN, &x, y, s.xend, tol, Nag_Relative,
NULLFN, NULLDFN, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_ode_ivp_bdf_gen (d02ejc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
printf("%8.2f", x);
printf("%13.4f%13.5f%13.4f\n", y[0], y[1], y[2]);
}
END:
nAG_FREE(y);
return exit_status;
}
static void nAG_CALL fcn(Integer neq, double x, const double y[], double f[],
Nag_User *comm)
{
struct user *s = (struct user *) comm->p;
if (s->use_comm[0]) {
printf("(User-supplied callback fcn, first invocation.)\n");
s->use_comm[0] = 0;
}
f[0] = y[0] * -0.04 + y[1] * 1e4 * y[2];
f[1] = y[0] * 0.04 - y[1] * 1e4 * y[2] - y[1] * 3e7 * y[1];
f[2] = y[1] * 3e7 * y[1];
}
static void nAG_CALL pederv(Integer neq, double x, const double y[],
double pw[], Nag_User *comm)
{
#define PW(I, J) pw[((I) -1)*neq + (J) -1]
struct user *s = (struct user *) comm->p;
if (s->use_comm[1]) {
printf("(User-supplied callback pederv, first invocation.)\n");
s->use_comm[1] = 0;
}
PW(1, 1) = -0.04;
PW(1, 2) = y[2] * 1e4;
PW(1, 3) = y[1] * 1e4;
PW(2, 1) = 0.04;
PW(2, 2) = y[2] * -1e4 - y[1] * 6e7;
PW(2, 3) = y[1] * -1e4;
PW(3, 1) = 0.0;
PW(3, 2) = y[1] * 6e7;
PW(3, 3) = 0.0;
}
static double nAG_CALL g(Integer neq, double x, const double y[],
Nag_User *comm)
{
struct user *s = (struct user *) comm->p;
if (s->use_comm[2]) {
printf("(User-supplied callback g, first invocation.)\n");
s->use_comm[2] = 0;
}
return y[0] - 0.9;
}
static void nAG_CALL out(Integer neq, double *xsol, const double y[],
Nag_User *comm)
{
struct user *s = (struct user *) comm->p;
printf("%8.2f", *xsol);
printf("%13.4f%13.5f%13.4f\n", y[0], y[1], y[2]);
*xsol = s->xend - (double) s->k * s->h;
s->k--;
}
