Keyword: 実一般矩形行列, LQ分解
概要
本サンプルは実一般矩形行列のLQ分解を行うC言語によるサンプルプログラムです。 本サンプルは以下に示される不定線形方程式をLQ分解を用いて解き、最小ノルム解を出力します。
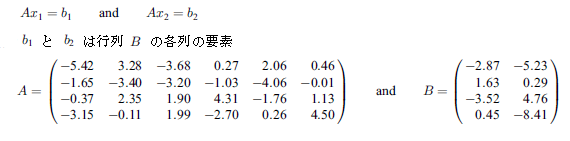
※本サンプルはnAG Cライブラリに含まれる関数 nag_dgelqf() のExampleコードです。本サンプル及び関数の詳細情報は nag_dgelqf のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_dgelqf のマニュアルページを参照)| このデータをダウンロード |
nag_dgelqf (f08ahc) Example Program Data 4 6 2 :Values of M, N and NRHS -5.42 3.28 -3.68 0.27 2.06 0.46 -1.65 -3.40 -3.20 -1.03 -4.06 -0.01 -0.37 2.35 1.90 4.31 -1.76 1.13 -3.15 -0.11 1.99 -2.70 0.26 4.50 :End of matrix A -2.87 -5.23 1.63 0.29 -3.52 4.76 0.45 -8.41 :End of matrix B
- 1行目はタイトル行で読み飛ばされます。
- 2行目に行列Aの行数(m)、列数(n)、右辺の数(nrhs)を指定しています。
- 3〜6行目に行列Aの要素を指定しています。
- 7〜10行目に行列Bの要素を指定しています。
出力結果
(本関数の詳細はnag_dgelqf のマニュアルページを参照)| この出力例をダウンロード |
nag_dgelqf (f08ahc) Example Program Results
Minimum-norm solution(s)
1 2
1 0.2371 0.7383
2 -0.4575 0.0158
3 -0.0085 -0.0161
4 -0.5192 1.0768
5 0.0239 -0.6436
6 -0.0543 -0.6613
- 5〜11行目に最小ノルム解が出力されています。
ソースコード
(本関数の詳細はnag_dgelqf のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_dgelqf (f08ahc) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*/
#include <stdio.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagf07.h>
#include <nagf08.h>
#include <nagx04.h>
int main(void)
{
/* Scalars */
Integer i, j, m, n, nrhs, pda, pdb, tau_len;
Integer exit_status = 0;
NagError fail;
Nag_OrderType order;
/* Arrays */
double *a = 0, *b = 0, *tau = 0;
#ifdef nAG_COLUMN_MAJOR
#define A(I, J) a[(J - 1) * pda + I - 1]
#define B(I, J) b[(J - 1) * pdb + I - 1]
order = Nag_ColMajor;
#else
#define A(I, J) a[(I - 1) * pda + J - 1]
#define B(I, J) b[(I - 1) * pdb + J - 1]
order = Nag_RowMajor;
#endif
INIT_FAIL(fail);
printf("nag_dgelqf (f08ahc) Example Program Results\n\n");
/* Skip heading in data file */
scanf("%*[^\n] ");
scanf("%ld%ld%ld%*[^\n] ", &m, &n, &nrhs);
#ifdef nAG_COLUMN_MAJOR
pda = m;
pdb = n;
#else
pda = n;
pdb = nrhs;
#endif
tau_len = MIN(m, n);
/* Allocate memory */
if (!(a = nAG_ALLOC(m * n, double)) ||
!(b = nAG_ALLOC(n * nrhs, double)) ||
!(tau = nAG_ALLOC(tau_len, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
/* Read A and B from data file */
for (i = 1; i <= m; ++i) {
for (j = 1; j <= n; ++j)
scanf("%lf", &A(i, j));
}
scanf("%*[^\n] ");
for (i = 1; i <= m; ++i) {
for (j = 1; j <= nrhs; ++j)
scanf("%lf", &B(i, j));
}
scanf("%*[^\n] ");
/* Compute the LQ factorization of A */
/* nag_dgelqf (f08ahc).
* LQ factorization of real general rectangular matrix
*/
nag_dgelqf(order, m, n, a, pda, tau, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dgelqf (f08ahc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Solve L*Y = B, storing the result in B */
/* nag_dtrtrs (f07tec).
* Solution of real triangular system of linear equations,
* multiple right-hand sides
*/
nag_dtrtrs(order, Nag_Lower, Nag_NoTrans, Nag_NonUnitDiag, m,
nrhs, a, pda, b, pdb, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dtrtrs (f07tec).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Set rows (M+1) to N of B to zero */
if (m < n) {
for (i = m + 1; i <= n; ++i) {
for (j = 1; j <= nrhs; ++j)
B(i, j) = 0.0;
}
}
/* Compute minimum-norm solution X = (Q^T)*B in B */
/* nag_dormlq (f08akc).
* Apply orthogonal transformation determined by nag_dgelqf (f08ahc)
*/
nag_dormlq(order, Nag_LeftSide, Nag_Trans, n, nrhs, m, a, pda,
tau, b, pdb, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dormlq (f08akc).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Print minimum-norm solution(s) */
/* nag_gen_real_mat_print (x04cac).
* Print real general matrix (easy-to-use)
*/
fflush(stdout);
nag_gen_real_mat_print(order, Nag_GeneralMatrix, Nag_NonUnitDiag, n, nrhs,
b, pdb, "Minimum-norm solution(s)", 0, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_gen_real_mat_print (x04cac).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
END:
nAG_FREE(a);
nAG_FREE(b);
nAG_FREE(tau);
return exit_status;
}
