Keyword: 陰的常微分方程式, 微分代数方程式, ODE, DAE
概要
本サンプルは微分代数方程式(DAE)を用いた陰的常微分方程式(ODE)の解を求めるC言語によるサンプルプログラムです。 本サンプルは以下に示される陰的形式で記述されるスティッフなRobertson問題を解いて結果を出力します。
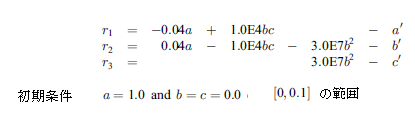
※本サンプルはnAG Cライブラリに含まれる関数 nag_dae_ivp_dassl_gen() のExampleコードです。本サンプル及び関数の詳細情報は nag_dae_ivp_dassl_gen のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
出力結果
(本関数の詳細はnag_dae_ivp_dassl_gen のマニュアルページを参照)| この出力例をダウンロード |
nag_dae_ivp_dassl_gen (d02nec) Example Program Results
t y(1) y(2) y(3)
0.0000 1.000000 0.000000 0.000000
(User-supplied callback res, first invocation.)
(User-supplied callback jac, first invocation.)
0.0200 0.999204 0.000036 0.000760
0.0400 0.998415 0.000036 0.001549
0.0600 0.997631 0.000036 0.002333
0.0800 0.996852 0.000036 0.003112
0.1000 0.996080 0.000036 0.003884
The integrator completed task, ITASK = 3
- 4〜9行目には独立変数の値と微分代数方程式の解が出力されています。
- 11行目に問題なく終了した積分により実行されたタスクが出力されています。"3"は解が要求される独立変数の値を超えて処理が進み積分が終了したことを意味します。
ソースコード
(本関数の詳細はnag_dae_ivp_dassl_gen のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_dae_ivp_dassl_gen (d02nec) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
/* Pre-processor includes */
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <nag.h>
#include <nag_stdlib.h>
#include <nagd02.h>
#ifdef __cplusplus
extern "C"
{
#endif
static void nAG_CALL res(Integer neq, double t, const double y[],
const double ydot[], double r[], Integer *ires,
Nag_Comm *comm);
static void nAG_CALL jac(Integer neq, double t, const double y[],
const double ydot[], double *pd, double cj,
Nag_Comm *comm);
static void nAG_CALL myjac(Integer neq, Integer ml, Integer mu, double t,
const double y[], const double ydot[],
double *pd, double cj);
#ifdef __cplusplus
}
#endif
int main(void)
{
/*Integer scalar and array declarations */
Integer exit_status = 0, maxord = 5;
Nag_Comm comm;
Integer neq, licom, mu, ml, lcom;
Integer i, itask, j;
Nag_Boolean vector_tol;
Integer *icom = 0;
NagError fail;
/*Double scalar and array declarations */
double dt, h0, hmax, t, tout;
double *atol = 0, *com = 0, *rtol = 0, *y = 0, *ydot = 0;
static double ruser[2] = { -1.0, -1.0 };
INIT_FAIL(fail);
printf("nag_dae_ivp_dassl_gen (d02nec) Example Program Results\n\n");
/* For communication with user-supplied functions: */
comm.user = ruser;
/* Set problem parameters required to allocate arrays */
neq = 3;
ml = 1;
mu = 2;
licom = 50 + neq;
lcom = 40 + (maxord + 4) * neq + (2 * ml + mu + 1) * neq +
2 * (neq / (ml + mu + 1) + 1);
if (!(atol = nAG_ALLOC(neq, double)) || !(com = nAG_ALLOC(lcom, double))
|| !(rtol = nAG_ALLOC(neq, double)) || !(y = nAG_ALLOC(neq, double))
|| !(ydot = nAG_ALLOC(neq, double))
|| !(comm.iuser = nAG_ALLOC(2, Integer))
|| !(icom = nAG_ALLOC(licom, Integer)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
/* Initialize the problem, specifying that the Jacobian is to be */
/* evaluated analytically using the provided routine jac. */
h0 = 0.0;
hmax = 0.0;
vector_tol = Nag_TRUE;
/*
* nag_dae_ivp_dassl_setup (d02mwc)
* Implicit DAE/ODEs, stiff ivp, setup for nag_dae_ivp_dassl_gen (d02nec)
*/
nag_dae_ivp_dassl_setup(neq, maxord, Nag_AnalyticalJacobian, hmax, h0,
vector_tol, icom, licom, com, lcom, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dae_ivp_dassl_setup (d02mwc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
/* Specify that the Jacobian is banded.
*
* nag_dae_ivp_dassl_linalg (d02npc)
* ODE/DAEs, ivp, linear algebra setup routine for
* nag_dae_ivp_dassl_gen (d02nec)
*/
nag_dae_ivp_dassl_linalg(neq, ml, mu, icom, licom, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dae_ivp_dassl_linalg (d02npc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
/* Set initial values */
t = 0.00e0;
tout = 0.00e0;
dt = 0.020e0;
for (i = 0; i < neq; i++) {
rtol[i] = 1.00e-3;
atol[i] = 1.00e-6;
y[i] = 0.00e0;
ydot[i] = 0.00e0;
}
y[0] = 1.00e0;
/* Use the comm.iuser array to pass the band dimensions through to jac. */
/* An alternative would be to hard code values for ml and mu in jac. */
comm.iuser[0] = ml;
comm.iuser[1] = mu;
printf(" t y(1) y(2) y(3)\n");
printf("%8.4f", t);
for (i = 0; i < neq; i++)
printf("%12.6f%s", y[i], (i + 1) % 3 ? " " : "\n");
itask = 0;
/* Obtain the solution at 5 equally spaced values of t. */
for (j = 0; j < 5; j++) {
tout = tout + dt;
/*
* nag_dae_ivp_dassl_gen (d02nec)
* dassl integrator
*/
nag_dae_ivp_dassl_gen(neq, &t, tout, y, ydot, rtol, atol, &itask, res,
jac, icom, com, lcom, &comm, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_dae_ivp_dassl_gen (d02nec).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
printf("%8.4f", t);
for (i = 0; i < neq; i++)
printf("%12.6f%s", y[i], (i + 1) % 3 ? " " : "\n");
/*
* nag_dae_ivp_dassl_cont (d02mcc)
* dassl method continuation resetting function
*/
nag_dae_ivp_dassl_cont(icom);
}
printf("\n");
printf(" The integrator completed task, ITASK = %4ld\n", itask);
END:
nAG_FREE(atol);
nAG_FREE(com);
nAG_FREE(rtol);
nAG_FREE(y);
nAG_FREE(ydot);
nAG_FREE(comm.iuser);
nAG_FREE(icom);
return exit_status;
}
static void nAG_CALL res(Integer neq, double t, const double y[],
const double ydot[], double r[], Integer *ires,
Nag_Comm *comm)
{
if (comm->user[0] == -1.0) {
printf("(User-supplied callback res, first invocation.)\n");
comm->user[0] = 0.0;
}
r[0] = (-(0.040e0 * y[0])) + 1.00e4 * y[1] * y[2] - ydot[0];
r[1] = 0.040e0 * y[0] - 1.00e4 * y[1] * y[2] - 3.00e7 * y[1] * y[1] -
ydot[1];
r[2] = 3.00e7 * y[1] * y[1] - ydot[2];
return;
}
static void nAG_CALL jac(Integer neq, double t, const double y[],
const double ydot[], double *pd, double cj,
Nag_Comm *comm)
{
Integer ml, mu;
if (comm->user[1] == -1.0) {
printf("(User-supplied callback jac, first invocation.)\n");
comm->user[1] = 0.0;
}
ml = comm->iuser[0];
mu = comm->iuser[1];
myjac(neq, ml, mu, t, y, ydot, pd, cj);
return;
}
static void nAG_CALL myjac(Integer neq, Integer ml, Integer mu, double t,
const double y[], const double ydot[], double *pd,
double cj)
{
Integer md, ms;
Integer pdpd;
pdpd = 2 * ml + mu + 1;
#define PD(I, J) pd[(J-1)*pdpd + I - 1]
/* Main diagonal PDFULL(i,i), i=1,neq */
md = mu + ml + 1;
PD(md, 1) = -0.040e0 - cj;
PD(md, 2) = -1.00e4 * y[2] - 6.00e7 * y[1] - cj;
PD(md, 3) = -cj;
/* 1 Subdiagonal PDFULL(i+1:i), i=1,neq-1 */
ms = md + ml;
PD(ms, 1) = 0.040e0;
PD(ms, 2) = 6.00e7 * y[1];
/* First superdiagonal PDFULL(i-1,i), i=2, neq */
ms = md - 1;
PD(ms, 2) = 1.00e4 * y[2];
PD(ms, 3) = -1.00e4 * y[1];
/* Second superdiagonal PDFULL(i-2,i), i=3, neq */
ms = md - 2;
PD(ms, 3) = 1.00e4 * y[1];
return;
}
