Keyword: 3次, スプライン, フィット
概要
本サンプルは3次スプライン曲線フィットを行うC言語によるサンプルプログラムです。 本サンプルは以下に示されるデータについてスプライン曲線フィットを行い、ノットの値とBスプライン係数を求めて出力します。
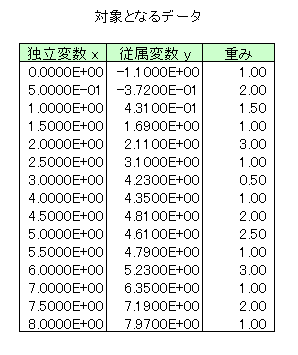
※本サンプルはnAG Cライブラリに含まれる関数 nag_1d_spline_fit() のExampleコードです。本サンプル及び関数の詳細情報は nag_1d_spline_fit のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はnag_1d_spline_fit のマニュアルページを参照)| このデータをダウンロード |
nag_1d_spline_fit (e02bec) Example Program Data 15 0.0000E+00 -1.1000E+00 1.00 5.0000E-01 -3.7200E-01 2.00 1.0000E+00 4.3100E-01 1.50 1.5000E+00 1.6900E+00 1.00 2.0000E+00 2.1100E+00 3.00 2.5000E+00 3.1000E+00 1.00 3.0000E+00 4.2300E+00 0.50 4.0000E+00 4.3500E+00 1.00 4.5000E+00 4.8100E+00 2.00 5.0000E+00 4.6100E+00 2.50 5.5000E+00 4.7900E+00 1.00 6.0000E+00 5.2300E+00 3.00 7.0000E+00 6.3500E+00 1.00 7.5000E+00 7.1900E+00 2.00 8.0000E+00 7.9700E+00 1.00 1.0 0.5 0.1
- 1行目はタイトル行で読み飛ばされます。
- 2行目にデータ点の数(m)を指定しています。
- 3〜17行目には独立変数x、従属変数y、重み(weights)を指定しています。
- 18〜20行目に平滑化因子(s)を指定しています。
出力結果
(本関数の詳細はnag_1d_spline_fit のマニュアルページを参照)| この出力例をダウンロード |
nag_1d_spline_fit (e02bec) Example Program Results
Calling with smoothing factor s = 1.000e+00
Number of distinct knots = 3
Distinct knots located at
0.0000 4.0000 8.0000
J B-spline coeff c
1 -1.3201
2 1.3542
3 5.5510
4 4.7031
5 8.2277
Weighted sum of squared residuals fp = 1.000e+00
Calling with smoothing factor s = 5.000e-01
Number of distinct knots = 7
Distinct knots located at
0.0000 1.0000 2.0000 4.0000 5.0000 6.0000
8.0000
J B-spline coeff c
1 -1.1072
2 -0.6571
3 0.4350
4 2.8061
5 4.6824
6 4.6416
7 5.1976
8 6.9008
9 7.9979
Weighted sum of squared residuals fp = 5.001e-01
Calling with smoothing factor s = 1.000e-01
Number of distinct knots = 10
Distinct knots located at
0.0000 1.0000 1.5000 2.0000 3.0000 4.0000
4.5000 5.0000 6.0000 8.0000
J B-spline coeff c
1 -1.0900
2 -0.6422
3 0.0369
4 1.6353
5 2.1274
6 4.5526
7 4.2225
8 4.9108
9 4.4159
10 5.4794
11 6.8308
12 7.9935
Weighted sum of squared residuals fp = 1.000e-01
- 3行目に呼び出される際の平滑化因子が出力されています。
- 5行目にノットの数が出力されています。
- 7〜9行目にノットの位置が出力されています。
- 12〜18行目にBスプライン係数が出力されています。
- 20行目に重みづけされた残差平方和が出力されています。
- 22行目に呼び出される際の平滑化因子が出力されています。
- 24行目にノットの数が出力されています。
- 26〜29行目にノットの位置が出力されています。
- 32〜42行目にBスプライン係数が出力されています。
- 44行目に重みづけされた残差平方和が出力されています。
- 46行目に呼び出される際の平滑化因子が出力されています。
- 48行目にノットの数が出力されています。
- 50〜53行目にノットの位置が出力されています。
- 56〜69行目にBスプライン係数が出力されています。
- 71行目に重みづけされた残差平方和が出力されています。
ソースコード
(本関数の詳細はnag_1d_spline_fit のマニュアルページを参照)
※本サンプルソースコードはnAG数値計算ライブラリ(Windows, Linux, MAC等に対応)の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
/* nag_1d_spline_fit (e02bec) Example Program.
*
* CLL6I261D/CLL6I261DL Version.
*
* Copyright 2017 Numerical Algorithms Group.
*
* Mark 26.1, 2017.
*
*/
#include <nag.h>
#include <stdio.h>
#include <nag_stdlib.h>
#include <nage02.h>
int main(void)
{
Integer exit_status = 0, j, m, nest, r;
NagError fail;
Nag_Comm warmstartinf;
Nag_Spline spline;
Nag_Start start;
double fp, s, *sp = 0, txr, *weights = 0, *x = 0, *y = 0;
INIT_FAIL(fail);
/* Initialize spline */
spline.lamda = 0;
spline.c = 0;
warmstartinf.nag_w = 0;
warmstartinf.nag_iw = 0;
printf("nag_1d_spline_fit (e02bec) Example Program Results\n");
scanf("%*[^\n]"); /* Skip heading in data file */
/* Input the number of data points, followed by the data
* points x, the function values y and the weights w.
*/
scanf("%ld", &m);
nest = m + 4;
if (m >= 4) {
if (!(weights = nAG_ALLOC(m, double)) ||
!(x = nAG_ALLOC(m, double)) ||
!(y = nAG_ALLOC(m, double)) || !(sp = nAG_ALLOC(2 * m - 1, double)))
{
printf("Allocation failure\n");
exit_status = -1;
goto END;
}
}
else {
printf("Invalid m.\n");
exit_status = 1;
return exit_status;
}
start = Nag_Cold;
for (r = 0; r < m; r++)
scanf("%lf%lf%lf", &x[r], &y[r], &weights[r]);
/* Read in successive values of s until end of data file. */
while (scanf("%lf", &s) != EOF)
{
/* Determine the spline approximation. */
/* nag_1d_spline_fit (e02bec).
* Least squares cubic spline curve fit, automatic knot
* placement, one variable
*/
nag_1d_spline_fit(start, m, x, y, weights, s, nest, &fp,
&warmstartinf, &spline, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_1d_spline_fit (e02bec).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
/* Evaluate the spline at each x point and midway
* between x points, saving the results in sp.
*/
for (r = 0; r < m; r++) {
/* nag_1d_spline_evaluate (e02bbc).
* Evaluation of fitted cubic spline, function only
*/
nag_1d_spline_evaluate(x[r], &sp[(r - 1) * 2 + 2], &spline, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_1d_spline_fit (e02bec).\n%s\n", fail.message);
exit_status = 1;
goto END;
}
}
for (r = 0; r < m - 1; r++) {
txr = (x[r] + x[r + 1]) / 2;
/* nag_1d_spline_evaluate (e02bbc), see above. */
nag_1d_spline_evaluate(txr, &sp[r * 2 + 1], &spline, &fail);
if (fail.code != NE_NOERROR) {
printf("Error from nag_1d_spline_evaluate (e02bbc).\n%s\n",
fail.message);
exit_status = 1;
goto END;
}
}
/* Output the results. */
printf("\nCalling with smoothing factor s = %12.3e\n", s);
printf("\nNumber of distinct knots = %ld\n\n", spline.n - 6);
printf("Distinct knots located at \n\n");
for (j = 3; j < spline.n - 3; j++)
printf("%8.4f%s", spline.lamda[j],
(j - 3) % 6 == 5 || j == spline.n - 4 ? "\n" : " ");
printf("\n\n J B-spline coeff c\n\n");
for (j = 0; j < spline.n - 4; ++j)
printf(" %3ld %13.4f\n", j + 1, spline.c[j]);
printf("\nWeighted sum of squared residuals fp = %12.3e\n", fp);
if (fp == 0.0)
printf("The spline is an interpolating spline\n");
else if (spline.n == 8)
printf("The spline is the weighted least squares cubic" "polynomial\n");
start = Nag_Warm;
}
/* Free memory allocated in spline and warmstartinf */
END:
nAG_FREE(spline.lamda);
nAG_FREE(spline.c);
nAG_FREE(warmstartinf.nag_w);
nAG_FREE(warmstartinf.nag_iw);
nAG_FREE(weights);
nAG_FREE(x);
nAG_FREE(y);
nAG_FREE(sp);
return exit_status;
}
