Keyword: 指数平滑化, ホルトウィンタース, 線形ホルト, 2重指数平滑化, Holt Winters
概要
本サンプルはC# (CSharp)により指数平滑化による予測を行うプログラムです。 入力データとして11個の観察データと指数平滑パラメータ(α、γ、φ)を与え、5ステップ分の予測を行います。
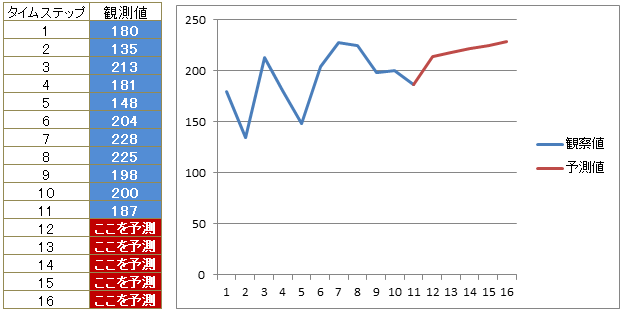
以下のプログラム例では線形ホルト指数平滑化を利用して予測を行いますが、その他に単純指数平滑化、ブラウン2重指数平滑化、ホルトウィンタース乗法、ホルトウィンタース加法の各平滑化法にも対応しています。
※本サンプルはnAG Library for .NETに含まれる関数 g13am()のExampleコードです。本サンプル及び関数の詳細情報はg13am のマニュアルページをご参照ください。
ご相談やお問い合わせはこちらまで
入力データ
(本関数の詳細はg13am のマニュアルページを参照)| このデータをダウンロード |
g13am Example Program Data 2 3 11 5 : MODE,ITYPE,N,NF 180 135 213 181 148 204 228 225 198 200 187 : Y 0.01 1.0 1.0 : PARAM(1:3) (since ITYPE=3) 11 : K (since MODE=2)
- 1行目はタイトル行で読み飛ばされます。
- 2行目では初期値の与え方 (mode=2)、平滑化の手法 (itype=3)、観察データ数 (n=11)、予測を行うステップ数 (nf=5)を与えます。コロン(:)以降は無視されます。
- 3行目で観察データ(y)の値を与えます。コロン(:)以降は無視されます。
- 4行目では指数平滑化パラメータ(param)にα(=0.01)、γ(=1.0)、φ(=1.0)を与えています。コロン(:)以降は無視されます。
- 5行目は初期値の推定に使用する観察データ数 (k=11)を与えています。コロン(:)以降は無視されます。
出力結果
(本関数の詳細はg13am のマニュアルページを参照)| この出力例をダウンロード |
g13am Example Program Results
Initial values used:
1 168.018
2 3.800
Mean Deviation = 2.5473e+001
Absolute Deviation = 2.1233e+001
Observed 1-Step
Period Values Forecast Residual
1 180.000 171.818 8.182
2 135.000 175.782 -40.782
3 213.000 178.848 34.152
4 181.000 183.005 -2.005
5 148.000 186.780 -38.780
6 204.000 189.800 14.200
7 228.000 193.492 34.508
8 225.000 197.732 27.268
9 198.000 202.172 -4.172
10 200.000 206.256 -6.256
11 187.000 210.256 -23.256
Forecast Standard
Period Values Errors
12 213.854 25.473
13 217.685 25.478
14 221.516 25.490
15 225.346 25.510
16 229.177 25.542
- 1行目はタイトルです
- 4〜5行目は計算に使われた初期値です。
- 7行目は平均偏差、8行目は絶対偏差で双方ともモデルの当てはまり具合を示しています。小さい値であればあるほど当てはまりが良いことを示します。
- 10行目〜23行目は観察値、1ステップ予測、及び残差を示します。
- 25行目〜32行目は5ステップ分の予測値とその標準誤差を示します。
ソースコード
(本関数の詳細はg13am のマニュアルページを参照)
※本サンプルソースコードは .NET環境用の科学技術・統計計算ライブラリである「nAG Library for .NET」の関数を呼び出します。
サンプルのコンパイル及び実行方法
| このソースコードをダウンロード |
// g13am Example Program Text
// C# version, nAG Copyright 2008
using System;
using NagLibrary;
namespace NagDotNetExamples
{
public class G13AME
{
static bool defaultdata = true;
static string datafile = "";
static void Main(String[] args)
{
if (args.Length == 1)
{
defaultdata = false;
datafile = args[0];
}
StartExample();
}
public static void StartExample()
{
try
{
DataReader sr = null;
if (defaultdata)
{
sr = new DataReader("exampledata/g13ame.d");
}
else
{
sr = new DataReader(datafile);
}
double ad, dv; int i, itype, ival, k, mode, n, nf, p;
int ifail;
Console.WriteLine("g13am Example Program Results");
//
// Skip headings in data file
k = 0;
sr.Reset();
// Read in the initial arguments and check array sizes
sr.Reset();
mode = int.Parse(sr.Next());
itype = int.Parse(sr.Next());
n = int.Parse(sr.Next());
nf = int.Parse(sr.Next());
double[] fse = new double[nf];
double[] fv = new double[nf];
double[] param = new double[4];
double[] res = new double[n];
double[] y = new double[n];
double[] yhat = new double[n];
if (n < 1 || nf < 1 )
{
Console.WriteLine(" ** Problem size is too small.");
goto L80;
}
sr.Reset();
for (i = 1; i <= n; i++)
{
y[i - 1] = double.Parse(sr.Next());
}
// Read in the itype dependent arguments (skipping headings)
if (itype == 1)
{
sr.Reset();
param[0] = double.Parse(sr.Next());
p = 0;
ival = 1;
}
else if (itype == 2)
{
sr.Reset();
param[0] = double.Parse(sr.Next());
param[1] = double.Parse(sr.Next());
p = 0;
ival = 2;
}
else if (itype == 3)
{
sr.Reset();
param[0] = double.Parse(sr.Next());
param[1] = double.Parse(sr.Next());
param[2] = double.Parse(sr.Next());
p = 0;
ival = 2;
}
else
{
sr.Reset();
param[0] = double.Parse(sr.Next());
param[1] = double.Parse(sr.Next());
param[2] = double.Parse(sr.Next());
param[3] = double.Parse(sr.Next());
p = int.Parse(sr.Next());
ival = p + 2;
if (p < 1)
{
Console.WriteLine("Problem size is too small.");
goto L80;
}
}
// Read in the mode dependent arguments (skipping headings)
double[] init = new double[ival];
double[] r = new double[p+13];
if (mode == 0)
{
// User supplied initial values
sr.Reset();
for (i = 1; i <= ival; i++)
{
init[i - 1] = double.Parse(sr.Next());
}
}
else if (mode == 1)
{
// Continuing from a previously saved R
sr.Reset();
for (i = 1; i <= p + 13; i++)
{
r[i - 1] = double.Parse(sr.Next());
}
}
else if (mode == 2)
{
// Initial values calculated from first K observations
sr.Reset();
k = int.Parse(sr.Next());
}
//
// Call the library method
G13.g13am(mode, itype, p, param, n, y, k, init, nf, fv, fse, yhat, res, out dv, out ad, r,
out ifail);
if (ifail != 0)
{
Console.WriteLine("** g13am failed with ifail = {0,5}", ifail);
goto L80;
}
// Display the output
Console.WriteLine("");
Console.WriteLine(" {0}", "Initial values used:");
for (i = 1; i <= ival; i++)
{
Console.WriteLine("{0,4} {1,12:f3} ", i, init[i - 1]);
}
Console.WriteLine("");
Console.WriteLine("{0}{1,12:e4}", "Mean Deviation = ", dv);
Console.WriteLine("{0}{1,12:e4}", "Absolute Deviation = ", ad);
Console.WriteLine("");
Console.WriteLine(" {0}", " Observed 1-Step");
Console.WriteLine(" {0}", " Period Values Forecast Residual");
Console.WriteLine("");
for (i = 1; i <= n; i++)
{
Console.WriteLine("{0,4} {1,12:f3} {2,12:f3} {3,12:f3}", i, y[i - 1], yhat[i - 1], res[i - 1]);
}
Console.WriteLine("");
Console.WriteLine(" {0}", " Forecast Standard");
Console.WriteLine(" {0}", " Period Values Errors");
Console.WriteLine("");
for (i = 1; i <= nf; i++)
{
Console.WriteLine("{0,4} {1,12:f3} {2,12:f3} ", n + i, fv[i - 1], fse[i - 1]);
}
//
L80: ;
//
}
catch (Exception e)
{
Console.WriteLine(e.Message);
Console.WriteLine("Exception Raised");
}
}
}
}
