単純な非線形最小二乗フィッティングの例

この例では、重み付き非線形最小二乗法を用いてデータをモデルにフィッティングする方法を示します。

handle_solve_bxnl (e04gg)は、nAG最適化モデリングスイートの境界制約付き非線形最小二乗信頼領域ソルバー(BXNL)で、小規模から中規模の問題を対象としています。以下の問題を解きます：

\[ \begin{array}{ll} {\underset{x \in \mathbb{R}^{n_{\text{var}}}}{minimize}\ } & \frac{1}{2} \sum_{i=1}^{n_{\text{res}}} w_i r_i(x)^2 + \frac{\sigma}{p}\|x\|^p_2\\ \text{subject to} & l_{x} \leq x \leq u_{x} \end{array} \]

ここで、\(r_i(x),i=1,\dots,n_{\text{res}}\)は残差と呼ばれる滑らかな非線形関数、\(w_i ,i=1,\dots,n_{\text{res}}\)は重み（デフォルトではすべて1に定義）、右端の項は正則化項で、パラメータ\(\sigma\geq0\)とべき乗\(p>0\)を持ちます。制約要素\(l_x\)と\(u_x\)は変数の境界を定義する\(n_{\text{var}}\)次元ベクトルです。

通常、キャリブレーションやデータフィッティングの文脈では、残差は\(t_i\)での観測値\(y_i\)と非線形モデル\(\phi(t;x)\)が提供する値との差として定義されます。つまり、\[r_i(x)≔y_i-\phi(t_i;x).\]

以下の例は、\(\alpha\)粒子のエッチングされた核トラックデータを畳み込み分布にフィッティングするためにe04ggを使用する方法を示しています。ターゲットシートをスキャンし、トラック直径（図1の赤いくさび）をヒストグラムに記録し、混合正規分布と対数正規分布モデルを実験ヒストグラムにフィッティングします（図2参照）。 PADC

図1: エッチングされた\(\alpha\)粒子トラックを持つPADC。

e04ggは、以下の6パラメータモデルをフィッティングするために使用されます： \[ \begin{array}{ll} \phi\big(t, x = (a, b, A_{\ell}, \mu, \sigma, A_g)\big) = \text{log-Normal}(a, b, A_l) + \text{Normal}(\mu, \sigma^2, A_g)\\ \text{subject to } 0 \leq x, \end{array}\] 図2に示されているヒストグラムの高さを使用します。

import numpy as np
import math
import matplotlib.pyplot as plt
from naginterfaces.base import utils
from naginterfaces.library import opt

# 問題データ
# 観測数
nres = 64
# 観測値
diameter = range(1, nres+1)
density = [
     0.0722713864, 0.0575221239, 0.0604719764, 0.0405604720, 0.0317109145, 
     0.0309734513, 0.0258112094, 0.0228613569, 0.0213864307, 0.0213864307,
     0.0147492625, 0.0213864307, 0.0243362832, 0.0169616519, 0.0095870206,
     0.0147492625, 0.0140117994, 0.0132743363, 0.0147492625, 0.0140117994,
     0.0140117994, 0.0132743363, 0.0117994100, 0.0132743363, 0.0110619469,
     0.0103244838, 0.0117994100, 0.0117994100, 0.0147492625, 0.0110619469,
     0.0132743363, 0.0206489676, 0.0169616519, 0.0169616519, 0.0280235988,
     0.0221238938, 0.0235988201, 0.0221238938, 0.0206489676, 0.0228613569,
     0.0184365782, 0.0176991150, 0.0132743363, 0.0132743363, 0.0088495575,
     0.0095870206, 0.0073746313, 0.0110619469, 0.0036873156, 0.0051622419,
     0.0058997050, 0.0014749263, 0.0022123894, 0.0029498525, 0.0014749263,
     0.0007374631, 0.0014749263, 0.0014749263, 0.0007374631, 0.0000000000,
     0.0000000000, 0.0000000000, 0.0000000000, 0.0000000000
     ]

# コールバック関数に渡されるデータ構造を定義する
data = {'d': diameter, 'y': density}

# PADCエッチトラック直径カウント（密度）のヒストグラムをプロットする
dh = np.arange(1, 10*nres+9)/10.0
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('PADC etch track diameter histogram', fontsize=16)
ax.set_xlabel('Diameter (nm)')
ax.set_ylabel('Density')
ax.set_xlim(xmin=1, xmax=65)
ax.bar(diameter, data['y'], color='lightsteelblue')
ax.grid()
plt.show()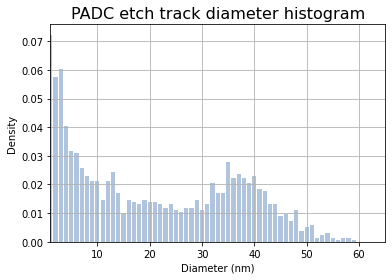

図2: α粒子のエッチングトラック直径のヒストグラム。棒グラフの高さは、集約モデル \(\phi(x, t)\) を用いてフィッティングされるデータです。

# 正規分布と対数正規分布を定義する
def lognormal(d, a, b, Al):
    return Al/(d*b*np.sqrt(2*math.pi))*np.exp(-((np.log(d)-a)**2)/(2*b**2))

def gaussian(d, mu, sigma, Ag):
    return Ag*np.exp(-0.5*((d-mu)/sigma)**2)/(sigma*np.sqrt(2*math.pi))

この問題を解決する観点から、最小化する関数は、モデル \(\phi(x;t)\) とデータペア（diameter, density）を使用した残差の合計です。パラメータベクトルは \(x = (a, b, A_l, \mu, \sigma, A_g)\) です。次のステップは、残差ベクトル \(\text{lsqfun}(x) := \big[r_1(x), r_2(x), \dots, r_{n_{\text{res}}}(x)\big]\) を返す関数を定義することです。

# 最小二乗関数を正規分布と対数正規分布の混合として定義する 
# 関数。また、その一次導関数を追加する
def lsqfun(x, nres, inform, data):
    """
    Objective function callback passed to the least squares solver.
    x = (a, b, Al, mu, sigma, Ag)
    """
    rx = np.zeros(nres)
    d = data['d']
    y = data['y']
    a = x[0]
    b = x[1]
    Al = x[2]
    mu = x[3]
    sigma = x[4]
    Ag = x[5]
    for i in range(nres):
        rx[i] = lognormal(d[i], a, b, Al) + gaussian(d[i], mu, sigma, Ag) - y[i]
    return rx, inform

def lsqgrd(x, nres, rdx, inform, data):
    """
    Computes the Jacobian of the least square residuals.
    x = (a, b, Al, mu, sigma, Ag)
    """
    n = len(x)
    d = data['d']
    a = x[0]
    b = x[1]
    Al = x[2]
    mu = x[3]
    sigma = x[4]
    Ag = x[5]
    for i in range(nres):
        # 対数正規分布の導関数
        l = lognormal(d[i], a, b, Al)
        # dl/da
        rdx[i*n+0] = (np.log(d[i])-a)/(b**2) * l
        # dl/db
        rdx[i*n+1] = ((np.log(d[i])-a)**2 - b**2)/b**3 * l
        # dL/dAl
        rdx[i*n+2] = lognormal(d[i], a, b, 1.0)
        # ガウス導関数
        g = gaussian(d[i], mu, sigma, Ag)
        # dμ/dμ
        rdx[i*n+3] = (d[i] - mu) / sigma**2 * g
        # dg/dsigma
        rdx[i*n+4] = ((d[i] - mu)**2 - sigma**2)/sigma**3 * g
        # dg/dAg
        rdx[i*n+5] = gaussian(d[i], mu, sigma, 1.0)
    return inform

# パラメータベクトル: x = (a, b, Al, mu, sigma, Ag)
nvar = 6

# モデルハンドルを初期化する
handle = opt.handle_init(nvar)

# 密な非線形最小二乗目的関数を定義する
opt.handle_set_nlnls(handle, nres)

# 各残差に重みを追加
weights = np.ones(nres)
weights[55:63] = 5.0
weights /= weights.sum()

# 測定値（重み）の信頼性を定義する
opt.handle_set_get_real(handle, 'rw', rarr=weights)

HandleSetGetRealReturnData(lrarr=64, rarr=None)

# パラメータ空間を制限する (0 <= x)
opt.handle_set_simplebounds(handle, np.zeros(nvar), 100.0*np.ones(nvar))

# ソルバーの出力を制御するためのオプションパラメータを設定する
for option in [
        'Print Options = NO',
        'Print Level = 1',
        'Print Solution = X',
        'Bxnl Iteration Limit = 100',
        'Bxnl Use weights = YES',
        # 3次正則化項を追加（過学習を回避）
        'Bxnl Reg Order = 3',
        'Bxnl Glob Method = REG',
]:
    opt.handle_opt_set(handle, option)

# 省略された反復出力のために明示的なI/Oマネージャーを使用する：
iom = utils.FileObjManager(locus_in_output=False)

# 初期推定値（開始点）を定義する
x = np.array([1.63, 0.88, 1.0, 30, 1.52, 0.24], dtype=float)

ソルバーを呼び出す

# ソルバーを呼び出す
slv = opt.handle_solve_bxnl(handle, lsqfun, lsqgrd, x, nres, data=data, io_manager=iom)

E04GG、境界制約付き問題に対する非線形最小二乗法状態: 収束、最適解が見つかりました目的関数の値 4.44211E-08 射影勾配のノルム 1.18757E-09 スケーリングされた射影勾配のノルム 3.98428E-06 ステップのノルム 1.66812E-01

プライマル変数: idx 下限値上限 1 0.00000E+00 2.02043E+00 1.00000E+02 2 0.00000E+00 1.39726E+00 1.00000E+02 3 0.00000E+00 6.93255E-01 1.00000E+02 4 0.00000E+00 3.65929E+01 1.00000E+02 5 0.00000E+00 7.01808E+00 1.00000E+02 6 0.00000E+00 3.36877E-01 1.00000E+02

最適解 \(x\) は、2つの分布（正規分布と対数正規分布、図4の青と赤の曲線）のアンフォールドされたパラメータを提供します。これらを合計すると、集計された曲線（図3と4の緑色で示されている）が生成され、これが最終的にフィッティングに使用されます。最適解は

# 最適なパラメータ値
# Al * log-Normal(a, b):
aopt = slv.x[0]
bopt = slv.x[1]
Alopt = slv.x[2]

# Ag * ガウス関数(mu, sigma):
muopt = slv.x[3]
sigmaopt = slv.x[4]
Agopt = slv.x[5]

そして目的関数の値は

print(slv.rinfo[0])

4.4421102582032486e-08

次の図3のプロットは、ヒストグラムに対する混合分布のフィッティングを示しています：

lopt = lognormal(dh, aopt, bopt, Alopt)
gopt = gaussian(dh, muopt, sigmaopt, Agopt)
w = lopt + gopt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('PADC etch track diameter histogram and fit', fontsize=16)
ax.set_xlabel('Diameter (nm)')
ax.set_ylabel('Density')
ax.set_xlim(xmin=1, xmax=65)
ax.bar(diameter, data['y'], color='lightsteelblue')
ax.plot(dh, w, '-', linewidth=3, color='tab:green')
ax.grid()
ax.legend(['Aggregated', 'Measured track diameter density'])
plt.show()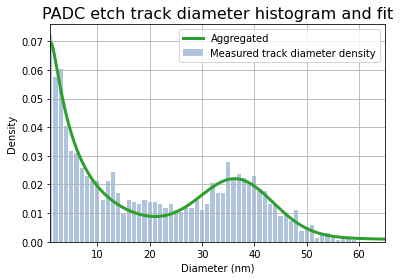

図3: 集計されたフィットを含むヒストグラム。

以下の図4は、展開されたフィットを示しています。赤色は対数正規分布、青色は正規分布を表しています：

fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_title('PADC etch track diameter histogram unfolding', fontsize=16)
ax.set_xlabel('Diameter (nm)')
ax.set_ylabel('Density')
ax.set_xlim(xmin=1, xmax=65)
ax.bar(diameter, data['y'], color='lightsteelblue')
ax.plot(dh, lopt, '-', linewidth=4, color='tab:red')
ax.plot(dh, gopt, '-', linewidth=4, color='tab:blue')
ax.plot(dh, w, '-', linewidth=3, color='tab:green')
ax.grid()
glab = 'Unfolded Normal($\\mu=%1.2f$, $\\sigma=%1.2f, A=%1.2f$)' % (muopt, sigmaopt, Agopt)
llab = 'Unfolded log-Normal($a=%1.2f$, $b=%1.2f, A=%1.2f$)' % (aopt, bopt, Alopt)
ax.legend([llab, glab, 'Aggregated', 'Measured track diameter density'])
plt.show()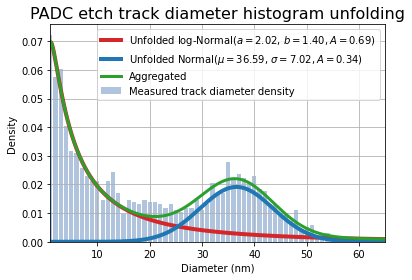

図4: フィッティングに使用された集約モデル（緑色の曲線）と展開されたモデル（青色と赤色の曲線）。最適なパラメータ値は凡例に記載されています。

最後に、クリーンアップしてハンドルを破棄します

# ハンドルを破棄する:
opt.handle_free(handle)

単純な非線形最小二乗フィッティングの例

nAG Library for Python Example集

単純な非線形最小二乗フィッティングの例