SQP マルチスタート

このノートブックは、nAG SQPソルバーを複数の開始点で使用して、グローバル最適化問題を解決する方法を示す短い例です。

ヒンメルブラウの関数を最小化します： \[ \min_{x,y} (x^2 + y - 11)^2 + (x + y^2 - 7)^2\\ -5 \leq x, y \leq 5 \]

まず、matplotlibを使用して実行可能領域上の関数をプロットすることから始めましょう：

# Jupyter の表示バックエンドを選択:
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.colors import LogNorm
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111)
X, Y = np.meshgrid(np.arange(-5.,5.,0.02), np.arange(-5.,5.,0.02))
Z = (X**2 + Y - 11)**2 + (X + Y**2 - 7)**2
lev = [0.1, 0.2, 0.5, 1., 2., 5., 10., 50., 100., 200., 500., 700., 1000., 2000.]
ax.contour(X, Y, Z, levels=lev, norm=LogNorm(), cmap=cm.plasma)
plt.show()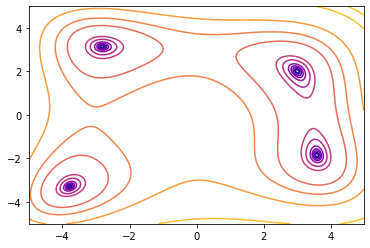

実行可能領域内にこの関数には4つの局所的最小値があり、すべての関数値は0.0であることがわかります。

ここで、ソルバーによって解かれる実際のモデルを定義することができます：

# 変数の範囲
bl = [-5., -5.]
bu = [5., 5.]
# 変数の数 
n = 2
# 必要な解の数
nb = 4
# 開始点の数
npts = 6

# 線形および非線形制約を制御するパラメータ（モデルでは単純な境界のみが定義されています）
ncnln = 0
repeat = False

# 目的関数コールバックに渡されるユーザーデータ
class usr_data:
    def __init__(self):
        self.npts = 0
        self.pts = []
        
def objfun(mode, x, objgrd, _nstate, data=None):
    # ヒンメルブラウ関数
    objf = (x[0]**2 + x[1] - 11)**2 + (x[0] + x[1]**2 - 7)**2
    if mode > 0:
        objgrd[0] = 4*x[0]*(x[0]**2 + x[1] - 11) + 2*(x[0] + x[1]**2 - 7)
        objgrd[1] = 2*(x[0]**2 + x[1] - 11) + 4*x[1]*(x[0] + x[1]**2 - 7)
    
    if data is not None:
        # 目的関数の評価を2回呼び出すごとに記録する
        data.npts += 1
        data.pts.append((x[0], x[1]))
    return objf, objgrd

from naginterfaces.base import utils
from naginterfaces.library import glopt
import warnings 

# ユーザーデータ、I/Oおよびオプションを初期化する
data = usr_data()
iom = utils.FileObjManager(locus_in_output=False)
warnings.simplefilter("error", utils.NagAlgorithmicWarning)
comm = {}
glopt.optset('Initialize = nlp_multistart_sqp', comm, io_manager=iom)
nsol = nb

# ソルバーを呼び出す
try:
    sln = glopt.nlp_multistart_sqp(
        n, ncnln, bl, bu, objfun, npts, repeat, nb, comm, data=data, 
        io_manager=None,
    )
except utils.NagAlgorithmicWarning as ex:
    if ex.errno == 8:
        sln = ex.return_data
        nsol = sln.info[nb-1]
    else:
        raise ex

print(nsol, 'solutions were found\n')

print('The', nsol, 'computed solutions are:')
for j in range(nsol):
    print("points coordinate: %6.3f, %6.3f, objective value: %6.3f"% (sln.x[0][j], sln.x[1][j], sln.objf[j]))

3 solutions were found

The 3 computed solutions are:
points coordinate:  3.000,  2.000, objective value:  0.000
points coordinate: -3.779, -3.283, objective value:  0.000
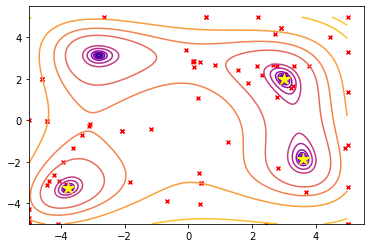
points coordinate:  3.584, -1.848, objective value:  0.000

評価された点を可視化するために、関数のレベルセットを再度プロットし、ソルバーによって要求された点のリストの散布図を追加しましょう:

fig = plt.figure()
ax = fig.add_subplot(111)
ax.contour(X, Y, Z, levels=lev, norm=LogNorm(), cmap=cm.plasma)
ax.scatter(*zip(*data.pts), s=15, marker='x', c='red')
for j in range(nsol):
    ax.plot(sln.x[0][j], sln.x[1][j], markersize=12, marker='*', c='yellow')
plt.show()

SQP マルチスタート

nAG Library for Python Example集

SQP マルチスタート