安定性
ある問題を解くための手法の安定性(stability)とは、その手法が求解プロセス中における(丸め)誤差にどの程度敏感に反応するかに関する特性を意味する。データが保証するのと同程度の解の精度を保証できる手法は安定であり、そうでないものは不安定である。条件(condition)が問題の鋭敏さに関係した概念であるのに対し、安定性は解法の鋭敏さに関係した概念である。
不安定な手法の具体例は標本分散を計算するための数式(3)
であるが、ここではさらに2つの例を追加する。
Example 4.9
(2次方程式)
2次方程式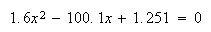 について考える。標準的な根の公式
について考える。標準的な根の公式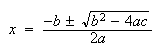 を使って有効桁数4桁の計算を行うと
を使って有効桁数4桁の計算を行うと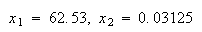 という解が得られる。しかし
という解が得られる。しかし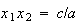 という関係式を使って
という関係式を使って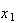 から
から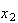 を求めると
を求めると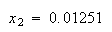 という別の結果が得られる。正しい解は
という別の結果が得られる。正しい解は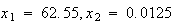 である。標準的な根の公式を用いた場合、小さい方の根については
である。標準的な根の公式を用いた場合、小さい方の根については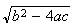 の値が
の値が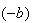 に近いものとなり、桁落ち(cancellation)が起るためこのような問題が生ずる。
に近いものとなり、桁落ち(cancellation)が起るためこのような問題が生ずる。
2次方程式の求解といった単純な問題であっても注意が必要である。関連する有用な情報については
Forsythe [1969]
を参照されたい。
Example 4.10
(漸化式)
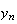 が
が
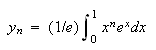
|
(7) |
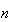 は非負の整数とする。区間
は非負の整数とする。区間![$[0,1]$](graphics/section4b__16.png) において
において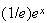 は
は より小さな値となるため、
より小さな値となるため、
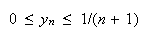
|
(8) |
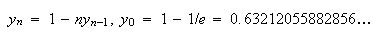
|
(9) |
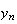 の値を求めるための魅力的な漸化式が得られたように見える。倍精度IEEE
arithmeticを前提としたとき、この前進漸化式を使って
の値を求めるための魅力的な漸化式が得られたように見える。倍精度IEEE
arithmeticを前提としたとき、この前進漸化式を使って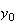 から
から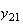 までの値を計算した結果を表tab2に示す。不等式(8)
に注意するなら、末尾の数項の値が正しい解から大きく乖離しつつあることがわかる。
までの値を計算した結果を表tab2に示す。不等式(8)
に注意するなら、末尾の数項の値が正しい解から大きく乖離しつつあることがわかる。
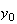 |
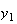 |
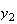 |
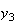 |
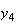 |
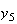 |
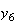 |
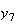 |
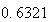 |
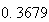 |
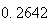 |
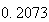 |
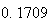 |
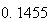 |
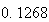 |
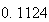 |
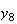 |
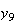 |
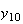 |
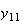 |
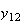 |
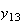 |
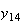 |
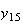 |
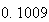 |
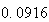 |
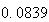 |
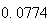 |
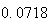 |
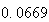 |
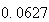 |
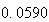 |
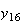 |
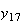 |
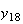 |
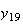 |
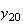 |
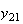 |
||
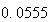 |
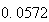 |
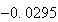 |
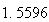 |
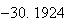 |
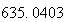 |
表2
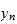 算出用漸化式
算出用漸化式
簡単な考察を行うことによってこの不安定性の理由を解明することができる。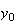 は厳密値では表現できないため、それからわずかにはずれた値
は厳密値では表現できないため、それからわずかにはずれた値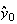 からスタートせざるを得ない。そこで
からスタートせざるを得ない。そこで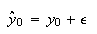 としよう。そうするとたとえその後の計算が厳密に行えたとしても
としよう。そうするとたとえその後の計算が厳密に行えたとしても
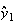 |
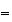 |
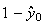 |
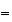 |
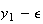 |
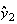 |
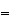 |
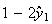 |
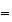 |
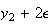 |
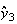 |
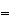 |
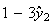 |
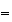 |
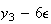 |
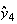 |
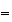 |
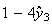 |
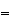 |
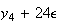 |
となる。一般式としては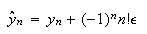 となることが帰納法によって証明できる。この場合、
となることが帰納法によって証明できる。この場合、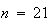 とすると
とすると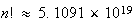 となる。これから明らかなように、この前進漸化式によって
となる。これから明らかなように、この前進漸化式によって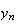 の値を計算する方法は誤差が急激に成長するために不安定である。
の値を計算する方法は誤差が急激に成長するために不安定である。
次に示すのはこの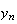 の値を計算するための安定な手法である。
の値を計算するための安定な手法である。
Example 4.11
(安定な漸化式)
数式
(9)
を変形することによって後退漸化式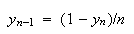 が得られる。今、
が得られる。今、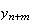 に対する近似値を
に対する近似値を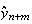 とする。
とする。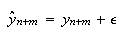
このときExample
4.10の場合と同様、次の一般式が得られる。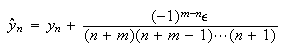
Example
4.10のときには誤差の急速な成長を招いたが、今回の場合、初期誤差は急速に減衰する。今、推定により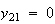 とすると
(8)
より
とすると
(8)
より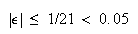
倍精度IEEE
arithmeticを前提に後退漸化式を用いると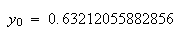 という値が得られる。これはここに表示した全桁数において正しい値である。これよりこの後退漸化式は安定であると言える。
という値が得られる。これはここに表示した全桁数において正しい値である。これよりこの後退漸化式は安定であると言える。
なお、
(7)
の積分は適切な数値積分公式を使うことによって問題なく安定的に値の評価が可能である。なぜなら関数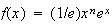 は区間
は区間![$[0,1]$](graphics/section4b__112.png) 全体で非負、単調だからである。
全体で非負、単調だからである。
常微分/偏微分方程式の解法においては、微分方程式を差分方程式で置き換えることに伴うある種の不安定性が発生する場合がある。最初に単純な非線形方程式の解法に伴う問題について触れておく。
Example 4.12
(寄生解)
方程式
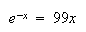
|
(10) |
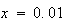 の近傍に解を持つ。
の近傍に解を持つ。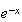 をべき級数に展開すると
をべき級数に展開すると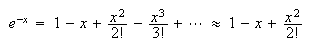 を得る。これより方程式
(10)
の近似解は2次方程式
を得る。これより方程式
(10)
の近似解は2次方程式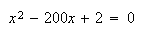 の一つの根として与えられる。ところでこの2次方程式は
の一つの根として与えられる。ところでこの2次方程式は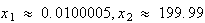 という2根を持つ。この2番目の根は元の方程式とは全く関係ないものであり、寄生解(parasitic
solution)と呼ばれる。
という2根を持つ。この2番目の根は元の方程式とは全く関係ないものであり、寄生解(parasitic
solution)と呼ばれる。
上の例の場合、寄生解が(10)
の解にならないことは明白であるため、それによってだまされることはない。しかし常微分/偏微分方程式の解法においては打切り誤差により、分離が明白ではないことが起る。
Example 4.13
(ODEの不安定性)
初期値問題
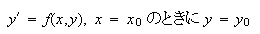
|
(11) |
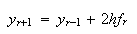
|
(12) |
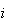 と
と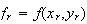 に対し
に対し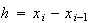 である。この手法の場合、打切り誤差は
である。この手法の場合、打切り誤差は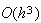 となる。
[Isaacson and Keller, 1966, Section 1.3, Chapter
8] (Note1) この手法は2つの開始値を必要とするため、一つの開始値は別の手段によって推定されなくてはならない。今、
となる。
[Isaacson and Keller, 1966, Section 1.3, Chapter
8] (Note1) この手法は2つの開始値を必要とするため、一つの開始値は別の手段によって推定されなくてはならない。今、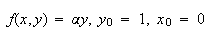 について考えることにする。この場合、
(11)
の解は
について考えることにする。この場合、
(11)
の解は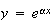 で与えられる。図6と図7は、
で与えられる。図6と図7は、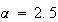 と
と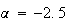 のそれぞれの場合につき、
のそれぞれの場合につき、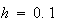 としたときの
(12)
によって得られた解を示したものである。いずれの場合も
としたときの
(12)
によって得られた解を示したものである。いずれの場合も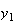 の値としては4桁の正しい値を設定してある。すなわち
の値としては4桁の正しい値を設定してある。すなわち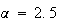 の場合には
の場合には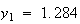 、
、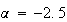 の場合には
の場合には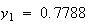 である。
である。
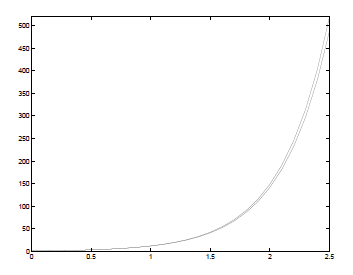
図6 ODEの例 -
安定な場合
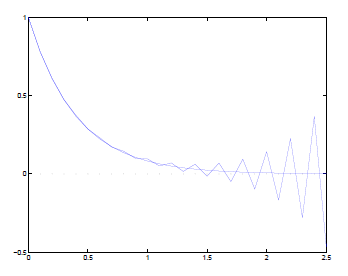
図7 ODEの例 -
不安定な場合
最初のケースについては数値解は厳密解に良く追従できている。しかし2番目のケースについては発振が見られ、数値解は厳密解から乖離してしまっている。
このような振舞いが生じる理由は (12) が
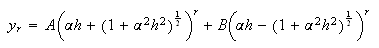
|
(13) |
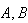 は初期条件に依存する定数である。初期条件
は初期条件に依存する定数である。初期条件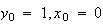 と
と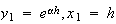 を与えた場合には、
を与えた場合には、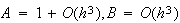 となる。
(13)
の第1項は厳密解を近似するものであるが、第2項は寄生解である。
となる。
(13)
の第1項は厳密解を近似するものであるが、第2項は寄生解である。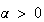 の場合、厳密解は増大し寄生解は減衰するため問題は起きない。しかし
の場合、厳密解は増大し寄生解は減衰するため問題は起きない。しかし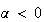 の場合には図7に示されるように、厳密解が減衰し寄生解が成長する。上記の現象に関するMilne-Simpson法というコンテキストでの興味深い議論については
Acton [1970, Chapter 5]
を参照されたい。数多くの助言や洞察に満ちた書籍である。より新しい
[Acton, 1996]
も同じ流れの本である。
の場合には図7に示されるように、厳密解が減衰し寄生解が成長する。上記の現象に関するMilne-Simpson法というコンテキストでの興味深い議論については
Acton [1970, Chapter 5]
を参照されたい。数多くの助言や洞察に満ちた書籍である。より新しい
[Acton, 1996]
も同じ流れの本である。
