プログラムの高速化・並列化サービスの事例:チューニングレポート：CITCOMのマルチグリッド法の改善

Ning Li, Numerical Algorithms Group
February 28, 2011

[2016年3月掲載]

イントロダクション

本プロジェクトの目的は、乱流の直接数値およびLarge-eddyシミュレーション(DNS/LES)を実行するIncompact3Dコードを、より現代的な形式にすることです。本作業は、コード開発者である、インペリアルカレッジの乱流・混相流・流体制御グループのChristos Vassilicos教授とSylvain Laizet博士とのコラボレーションで行いました。本プロジェクトの中心となる目標は、Incompact3Dの通信ルーチンの書き換えです。特にその領域分割手法を1Dスラブ分割から2Dペンシル分割へアップデートして、現代的なスーパーコンピューターであるHECToR上でのスケーラビリティ改善を行うことが目的です。

本プロジェクトは、16人月の計画で、2009年4月に開始されました。プロジェクトの早い段階において、他のアプリケーション、特に空間的に陰的スキームを用いる3DカルテシアンメッシュCFDコードにとって、本作業の成果が役に立つことが解りました。最終的に、その再利用可能なソフトウェア部品は、 2DECOMP&FFTと呼ぶライブラリにまとめられ、他の研究コミュニティーに広く提供されることとなりました。

2DECOMP&FFTは、2つの主要な機能を持つFortranライブラリです。これは、低レベルとしては、 3Dカルテシアンデータ構造を用いるアプリケーションのための、2D領域分割アルゴリズム（ペンシル'pencil'あるいは'drawer'領域分割とも呼ばれます)を実装しています。さらに高レベルでは、3次元分散FFT実行のための単純で効率的なFFTインターフェイスも提供します。このライブラリは、スーパーコンピューターでの大規模計算に最適化されており、数千プロセッサーまでスケールします。これはMPIをベースにしていますが、ユーザーフレンドリーなインターフェイスを持ち、開発者は通信の詳細に立ち入る必要はありません。

Incompact3Dは、その新しい領域分割手法により、HECToRの16384コアに対して性能はスケールし、高い並列効率を可能にします。これは研究グループの生産性を大きく向上させました。またそのライブラリ開発も優れたアイデアとして認められました。本プロジェクトとは別に、2DECOMP&FFTを燃焼コードDSTARへ組み込む等の別のプロジェクトが並行して開始されました。

本レポートの残りの部分は以下のような構成です。セクション2では、 2D領域分割手法の概略を示します。セクション3では、2DECOMP&FFTライブラリを簡単に紹介します。セクション4では、2DECOMP&FFTの領域分割APIを示します。セクション5では、 HECToRで用いる事の出来る様々な並列FFTソフトウェアをレビューします。

セクション6では、2DECOMP&FFTのFFTのAPIを、セクション7では、その並列性能を示します。 HECToRのような現代的なスーパーコンピューターでは、共有メモリープログラミングが増々ポピュラーになっています。 2DECOMP&FFTでは共有メモリー実装が基本であり、セクション8でそれを議論します。セクション9では、 CFDアプリケーションIncompact3Dの数値計算アルゴリズムを紹介します。

特に、圧力ポアソン方程式のスペクトル解法とその実装について議論します。このセクションでは新しいIncompact3Dの性能も示します。最後に結論と今後をセクション10で纏めます。

2　　2D領域分割

このセクションの議論は、空間的に陰的スキームを用いた、3Dカルテシアンメッシュをベースにする他のアプリケーションにも当てはまるものです。例えば、コンパクトな有限差分法は多くの場合、空間的な微分や補間を行う際に、三重対角線形システムを解くことになります。また、スペクトル法コードは多くの場合、グローバルなメッシュラインに沿ったFFTを実行します。

分散メモリーシステム上でこのような計算を行うには2通りの方法があります。一つは、分散アルゴリズム（例えば、並列三重対角行列ソルバーや、分散データ上の並列FFT)、あるいは動的にプロセッサー間でデータを再配置(転置)してローカルメモリー上でシリアル実行する方法です。二つ目は、その簡明さからよく用いられる方法です：既存のシリアル実行コード（既にシングルCPUで最適化されていることが望ましい)はそのままで（元のロジックがそのままである限りにおいて移植は直截的に行えます)、追加するのはデータ転置手続きのみ、という方法です。

スーパーコンピューター利用の初期のころは、多くのアプリケーションは上記のアイデアを1D領域分割（スラブ領域分割として知られています)で実装していました。図1に、XとY方向に分割された3D領域を示します。図(a)では、X-Y平面内の計算はローカルで行われ、Y方向のメッシュラインで分散されます。もしYメッシュラインを跨った計算が必要になった場合は(Y方向の微分やY方向の1D FFT)、プロセッサー間でデータを図(b)となるように再配置すれば、Y方向の計算をローカルに実行できます。標準的なMPIライブラリを用いる場合、(a)と(b)間の交換はMPI_ALLTOALL(V)を用いれば可能です。

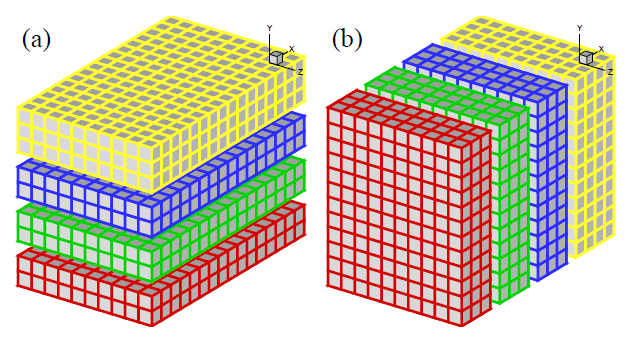
図1：4プロセッサーを用いる場合の1D領域分割：(a)Y方向で分割、(b)X方向で分割

1D領域分割は極めて単純ですが、特に大規模シミュレーションにおいては限界があります。サイズN³の立方体メッシュにおいて明らかな制約は、用いる事の出来る最大のプロセッサー数N_procはNであり、各スラブは少なくとも1枚の平面です。10億ポイントの立方体メッシュでは、この制約はN_proc<=1,000コアです。これは、10,000コア以上あるいは物によっては10,000コア以上を搭載する現代的なスーパーコンピュータにとっては厳しい制約です。大規模計算においては、各プロセッサーの負荷が大きすぎ、そのメモリーの制限に達してしまいます。

2D領域分割(ペンシル領域分割とも呼ばれる)は、1D領域分割の自然な拡張です。図2は、図1の3D領域が2つの次元で分割される様子を示しています。

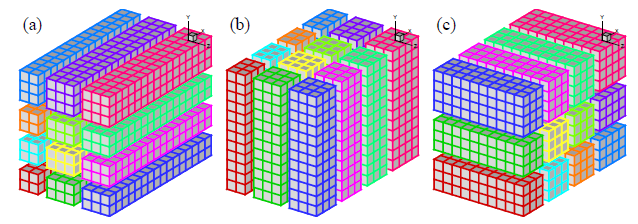
図2：4×3プロセッサーを用いる場合の2D領域分割

ここでもMPI_ALLTOALL(V)を用いてデータ転置が可能です。しかしながら、1Dの場合に比べて格段に複雑です。ここには2つの異なるコミュニケーターグループが必要です。P_row×P_colプロセッサーグリッドに対して、P_row個のP_colプロセッサーグループは、(a)<=>(b)で自身の間でデータを交換する必要があり、P_col個のP_rowプロセッサーグループは、(b)<=>(c)で自身の間でデータを交換する必要があります。

一方、通信ルーチンの実装は極めて技巧的です。例えば、通信はペンシルの方向とそのメモリーパターンに依存しています。MPIライブラリのメモリーバッファのパッキングとアンパッキングは、効率に対して注意深く扱う必要があります。これらのソフトウェア工学的な話題は、このアプリケーションによる科学的研究とはほとんど関係のない事柄です。

他方、この2D領域分割手法は以前から知られていましたが、実アプリケーションへの採用が見直されたのは最近になってからの事で、一般の研究者がスーパーコンピューターの数千コアを日常的に用いる事が実際に期待できるようになったその時、1D領域分割のメモリー制約に直面したためです。事実、著者は、英国のCFDコミュニティーでさえ10個に及ぶアプリケーションが、こうしたアップグレードをすぐにでも必要とされていることに気づきました。

こうした状況が、2DECOMP&FFTライブラリの開発動機です。本プロジェクトの範囲を超えて、再利用される一般目的のライブラリとして開発し、これら技術的課題に対応させて、アプリケーション開発にソフトウェア工学的な詳細に立ち入ることなく、研究者はその研究自身に専念することが可能になります。

3 2DECOMP&FFTの概要

2DECOMP&FFTライブラリは、2種のレイヤーから設計されています。一つは、データ分散に基礎を置いた一般目的の2D領域分割で、もう一つは、3次元並列FFTインターフェイスです。実際に、多くの数値計算アルゴリズムは2D領域分割ライブラリを基礎に構築されています。よってソフトウェの枠組みとして2DECOMP&FFTを呼出す方式が好ましい形式です。例えば、大規模スペクトルコードは、フーリエ級数でなく基底関数を用いて構築することが可能です（境界条件によっては、ヤコビあるいはチェビシェフ基底関数を用いる場合があります）。セクション9で述べるように、楕円型PDEソルバーもこの枠組みを用いて構築することが可能です。

2DECOMP&FFTは標準的なFortranで記述されています。ライブラリのビルドには、Fortran95互換コンパイラーが要求されます（このコードは、ISO TR 15581で定義されるallocatableアレイ仕様やCrayポインターも用いており、これらは良く知られたFortran拡張で、ほとんどのFortranコンパイラーでサポートされているものです)。通信コードは標準的なMPIをベースにしています。FFTインターフェイスに柔軟性を持たせ、サードパーティーのFFTライブラリを用いて2DECOMP&FFTはデータ分散のみをハンドリングさせて利用することが可能なようにしています。このライブラリとアプリケーションは、他のハードウェアへ移植が容易なように構築されています。実際に、Incompact3Dは、少ない作業量で幾つかの他のプラットフォーム(Cray,IBM,SGI)へすでに移植されています。

HECToR上では、2DECOMP&FFTのバイナリー形式が以下の場所にインストールされています。


/usr/local/packages/nag/2decomp_fft/1.0.237/

実際に動かすには、sampleディレクトリーに在るテストアプリケーションから試すことが出来ます。例えば、サンプルコードtest2d.f90をコンパイルするには、それを各自の作業ディレクトリーへコピーし、以下のようにします


export DECOMP2D_DIR=/usr/local/packages/nag/2decomp_fft/1.0.237/
ftn -I$DECOMP2D_DIR/include test2d.f90 -L$DECOMP2D_DIR/lib -l2decomp
-l2decomp_fft -o test2d.exe

ただし、このバイナリー形式は、PGIでビルドされたテスト目的のみに用いるもので、単精度のみのFFT実装が施されています。完全なオプションにアクセスするには、ソースパッケージを入手して、FFTWやACMLFFTのようなより効率的なFFTエンジンを用いてビルドしてください。

dCSEプロジェクトの精神に従い、ソースコードはHECToRユーザーに公開されています。また、このソフトウェアは、Open Petascale Libraries(http://www.openpetascale.org/)の一部となり、ソースコードはオープンソースライセンスの元に公開されています。

4 2D領域分割のAPI

2DECOMP&FFTライブラリは、数種のFortranモジュールで提供されます。ベースモジュールは2D領域分割とデータ分散ルーチンから構成されます。その他に、FFTモジュールは3次元並列FFT関数を提供します。更に、並列I/OのためのMPI-IOモジュール等のユーティリティー関数も有ります。領域分割ライブラリはこのセクションで、FFTインターフェイスはセクション6で議論します。

4.1 2D領域分割の基本API

このサブセクションでは、2D領域分割ライブラリのpublicインターフェイスを説明します。本セクションを読めば、この領域分割手法によるアプリケーション構築が容易になるでしょう。ライブラリのインターフェイスは非常に簡単です。サンプルアプリケーションから始めましょう。

まず最初に、アプリケーションの先頭に以下のFortranモジュールをインクルードします。


use decomp_2d

ライブラリのpublicインターフェイスは、グローバル変数のセットとしてグローバルデータを如何に分散するかという領域分割情報を含み、アプリケーションにはそのデータ構造定義が必要です。以下の初期化処理の後には、全てのグローバルデータをread-onlyにします：


call decomp_2d_init(nx,ny,nz,P_row,P_col)

ここで、nx,ny,nzは3Dグローバルデータサイズで、P_row,P_colは分散対象の2DプロセッサーグリッドサイズP_row×P_colです。ここで、いかなる次元もP_rowあるいはP_colで割り切れる必要はないことに注意してください。しかしながら、性能劣化を引き起こす負荷分散を避けるように選ぶべきです。次の制約にも注意してください：P_row≤min(nx,ny)およびP_col≤min(ny,nz)。

以下はアプリケーションで用いるグローバル変数のリストです。これら変数名は、競合を避けるためにアプリケーション内で再定義されないようにすべきです（Fortranモジュールのpublicグローバル変数使用は、常に最善策とは言えません。しかしながらこの設計は、このライブラリでアプリケーションの構築を簡素化することを意図して行いました)。また、幾つかの変数は重複かつ冗長な情報を含んでいますが、これはプログラミングを容易にするためのものです。

mytype：浮動小数点データの種別を定義するのに用います。例えば、real(mytype) :: varあるいはcomplex(mytype) :: cvar、と言った具合です。これは、単精度/倍精度の変更を容易にします。
real_type,complex_type：それぞれ実数および複素数のMPIのデータ型として、アプリケーションが直接MPIライブラリルーチンを呼出す際に用います。
nx_global,ny_global,nz_global：グローバルデータのサイズ。
nproc：MPIランク総数。
nrank：現状のプロセッサーのMPIランク。
xsize(i),ysize(i),zsize(i),i=1,2,3：現状のプロセッサーが受け持つサブ領域サイズ。最初の文字はペンシル方向を表し、その1D配列要素はx,y,z方向のサブ領域サイズです。2D領域分割においては、完全にローカルメモリーに配置される1次元が常に存在します。よって以下のように定義されます：xsize(1)==nx_global,ysize(2)==ny_global,zsize(3)==nz_global。
xstart(i),ystart(i),zstart(i),xend(i),yend(i),zend(i),i=1,2,3：グローバル座標系における、各サブ領域の開始/終了インデックス。明らかに、xsize(i)=xend(i)-xstart(i)+1となります。3D領域から2D平面を展開する場合のような、グローバル座標を用いるアプリケーションに便利な変数です。

領域分割ライブラリの初期化後すぐに、メインプログラムにおいてグローバル変数の主要なデータ構造を定義することが推奨されます。Allocatable配列を用いる方が良いですが、以下のようにサブルーチン内の静的配列を用いる事も可能です：


! allocate a X-pencil array
allocate(var(xsize(1), xsize(2), xsize(3)))
! allocate a Y-pencil array using global indices
allocate(uy(ystart(1):yend(1), ystart(2):yend(2), &
ystart(3):yend(3)))
! define a Z-pencil work array in a subroutine
real, dimension(zsize(1),zsize(2),zsize(3)) :: work1

データの転置を実行する通信ルーチン群が、ライブラリの重要な要素です。セクション2で示したように、実際の計算では、3方向のペンシル間の4つのグローバル転置操作が必要です。これに対応して、ライブラリは4つの通信ルーチンを提供します：


call transpose_x_to_y(in, out)
call transpose_y_to_z(in, out)
call transpose_z_to_y(in, out)
call transpose_y_to_x(in, out)

入力配列inを出力配列outは、呼出しプログラムで正しいペンシル方向に対して定義されなければなりません。

ライブラリはFortranのgenericインターフェイスで記述されているため、異なるデータ型をユーザーの手を煩わせずにサポートされます。つまりこのinとoutは実数配列でも複素数配列でも良く、後者はFFTタイプのアプリケーションに便利です。

こうして、通信の詳細はブラックボックスに隠され、アプリケーション開発者はこれら転置ルーチンの内部ロジックを把握する必要はありません。しかしながら通信ルーチンは高価な処理であり、大規模プロセッサー上で動作する場合は特にそうです。よってこれらを呼出す回数を、アルゴリズムの工夫や計算と重複させるなどにより、最小限にすべきです。最後に、実行完了の前にメモリーをクリアします：


call decomp_2d_finalize

4.2 より進んだ2D領域分割API

基本APIは大変ユーザーフレンドリーなものですが、より複雑なデータ構造を扱う必要がある場合もあります。CFDアプリケーションで良くある状況は、スタッガードメッシュのようなグローバル変数に対して異なる保存が必要となる場合です(セル中心とセル境界)。他の例は、real-to-complex FFTを用いる場合で、アプリケーションは実数入力（グローバルサイズのnx*ny*nz)と複素数出力（より小さいサイズ(nx/2+1)*ny*nz：出力の約半分は複素共役対称性のため落とされる)の両方を保存しなくてはなりません。

アプリケーションは、異なるデータセットを2Dペンシルとして分散できなくてはなりません。2DECOMP&FFTは、こうした状況に対して強力かつ柔軟なプログラミング・インターフェイスを提供します：


TYPE(DECOMP_INFO) :: decomp
call decomp_info_init(mx, my, mz, decomp)

ここでdecompは、特定のグローバルサイズに関連する2D領域分割情報をカプセル化した、Fortranの派生データ型DECOMP_INFOのインスタンスです。このオブジェクトはdecomp_info_initルーチンで初期化され、基本APIインターフェイスの3番目のパラメーターとして通信ルーチンへ渡されます：


call transpose_x_to_y(in, out, decomp)

第3パラメーターはオプショナルな引数で、基本インターフェイスのみ用いた場合は無視されます。これが使用されている場合は、デフォルトのグローバルサイズnx*ny*nzの代わりに、関連するグローバルサイズを用いてグローバル転置が適用されます。

5 FFTパッケージのレビュー

高速フーリエ変換：FFTは、多くの科学技術計算アルゴリズムの基礎を提供します。数多くのFFTソフトウェアパッケージが存在しますが、本セクションでは、本プロジェクトに関連するもの、特にCrayシステムで動作するもののみをレビューします。

5.1 並列FFTパッケージ

FFTW[3]は、最も良く知られたFFTパッケージの一つです。オープンソースで、任意の入力を許し、ポータブルで、セルフチューニング設計（planning before execution)により良好な性能を提供します。FFTWには2つの主要なバージョンがあります。バージョン2.xは、分散データ変換にMPIインターフェイスを用います。しかしながら、内部的には1D(スラブ)領域分割を用いており、以前に議論したように、これは計算規模の制約が生じます。シリアル実行性能も、現代的なCPUのSIMD命令をサポートするバージョン3.xに劣ります。残念ながらバージョン3.xのMPIインターフェイスは長期に渡って不安定な状態が続いています。よって多次元並列FFTで信頼のおける方法がありません。
CRAFFT(Cray Adaptive FFT)は、例えばXT/XEシステム上のxt-libsciの一部として、Crayシステムで動作します。これは他のFFTカーネル(FFTWを含む)へ計算を委譲する簡単化されたインターフェイスを持ちます。この'adaptive'という言葉は、システム上の最速のFFTカーネルを動的に選択することを意味します。しかしながらこれは、極めて特殊なルーチン（xt-libsciバージョン10.5.0では2D/3Dのcomplex-to-complex変換のみサポートされています)のみをサポートしており、さらにこれらは並列1D領域分割のみをベースにしています。

2D領域分割ベースの並列FFTを実装する利用可能なオープンソースとして以下のものがあります：

Plimptonの並列FFTパッケージ[8]は、2D/3Dのcomplex-to-complex FFTのCルーチンセットで、データ転置に対して極めて柔軟な再配置ルーチンを持っています。通信はMPI_SENDとMPI_IRECVで実装されています。
TakahashiのFFTEパッケージ[1]は、FORTRANで記述されており、complex-to-complex FFTのシリアルおよび並列版が含まれます。小さな素因数のみで長さを変換し、MPI_ALLTOALLを用いて分散データを一律に転置します。ユーザーが呼出し可能な通信ルーチンはありません。
P3DFFT[6]は最も良く知られたオープンソース並列FFTライブラリです。このライブラリは、UCSD・サンディエゴ・スーパーコンピューターセンターのDmitry Pekurovskyにより開発されました。これは極めて高性能で、広く科学者の間で、最先端の乱流研究を含む大規模シミュレーションに適用されています。
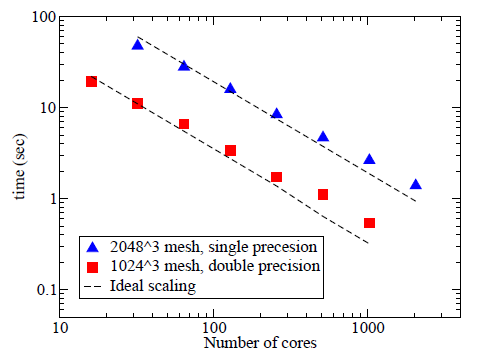
図3：HECToRフェーズ1上でのP2DFFTのスケール性能
P3DFFTは、本プロジェクトの初期段階でHECToRへ移植されています。図3は、デュアルコアでの良好なスケール性能を示しています。これに対して、新たなライブラリ開発が必要な理由を以下に示します：
1. P2DFFTはFFTのみのパッケージである。一般目的の2D領域分割ライブラリとして設計されておらず、通信ルーチンをユーザーが利用できるように作られていません。セクション9で見るように、Incompact3Dには、より複雑なデータ分散処理の一般目的のライブラリが必要です。
2. P3DFFTは、スペクトル変換アプリケーションに特化しており、real-to-complexとcomplex-to-real変換のみを実装しています。2DECOMP&FFTは、更にcomplex-to-complex変換も実行が可能です。
3. 2DECOMP&FFTの通信レイヤーとFFTレイヤーの分離は、より低レベルの通信コードが必要なライブラリの追加を可能にしています（チェビシェフ基底関数やヤコビ基底関数による変換や、一般目的のポアソン・ソルバー：セクション9で議論されます)。
本文書作成の終了の時点で、新しいPFFTパッケージが発表されました。このパッケージは、大規模並列アーキテクチャー上で、並列complex-to-complex変換を計算します。C言語で記述され、FFTW3.3alpha1をベースにしています。極めて柔軟なデータレイアウトをサポートし、P3DFFTよりも高速であると謳っています。

5.2 シリアルFFT実装

並列FFTインターフェイスは、データ管理と通信のみ担当します。実際の1DFFT計算は、単一CPUコア上で十分に最適化されていると考えて、サードパーティーFFTライブラリに任せます。現状ユーザーは、コンパイル時に下記の6種のFFTの中から選択することが出来ます：

Generic：2DECOMP&FFTのポータビリティーのために、汎用アルゴリズムがデフォルトのFFTエンジンとして備わっています。このアルゴリズムはGlassman[5][11]のよるものです。
FFTW：Cray XT/XEで正式にサポートされています。本実装では、FFTW APIのバージョン3.xを用います。
ACML：AMD社のCPU向けのベンダーライブラリです。そのFFTカーネルは、アセンブリ言語で書かれ、高度に最適化されています。
FFTPACK:古いアプリケーションで広く使われています。バージョン5.0の実装は、Fortran90に基づいています[2]。
ESSL：POWERx系やBlueGenesを含むIBMシステム向けの実装です。
MKL：Intel系CPUを用いたシステム向けの実装です。Intel社にはラッパーを提供していただき感謝します。これはFFTWの代わりにMKLを呼出すもので、上述のFFTW実装を直接MKLへリンクすることが可能です。

更に要求があれば他のFFTエンジンもサポート可能です。実際に、単純な1DシリアルFFTの計算を提供する任意のサードパーティ製のFFTライブラリをラップすることは可能です。

6 FFT API

FFTプログラミングインターフェイスの利用に際しては、まず最初にFortranモジュールの追加から始めます。


use decomp_2d_fft

当初注意したように、FFTインターフェイスは、2D領域分割ライブラリ上に構築されているため、最初に初期化が必要です。


call decomp_2d_init(nx,ny,nz,P_row,P_col)

次にFFTインターフェイスの初期化を行います：


call call decomp_2d_fft_init

初期化ルーチンは、FFTエンジンのプランニングを行い(サポートされている場合)、計算のための(テンポラリー作業領域などの)グローバルデータ構造を決定します。デフォルトでは、物理的-空間データはXペンシルに保存されると仮定します。対応するスペクトル-空間データは、FFT後に転置されたZペンシル形式で保存されます。アプリケーションをより柔軟なものとするために、ライブラリはその反対方向もサポートします。これは以下のようにオプショナル・パラメーターを初期化ルーチンへ渡して指示します：


call decomp_2d_fft_init(PHYSICAL_IN_Z)

Yペンシルの物理的-空間データはオプションにはありません。それは更に高価な計算を要し、経済的ではないためです。

このFFTパッケージが提供する主たる機能は3D FFTであり、分散された入力データは、プロセッサーを跨って通常のijk順序の3D配列に保存されます。complex-to-complex(c2c)FFTのユーザーインターフェイスは以下のものです：


call decomp_2d_fft_3d(in, out, direction)

ここで、directionは、順変換ではDECOMP_2D_FFT_FORWARD、逆変換ではDECOMP_2D_FFT_BACKWARDのどちらかです。入力配列inと出力配列outは共に複素数で、Xペンシル/Zペンシルという組合せかその逆のどちらかです。これはFFTの方向と、FFTインターフェイスの初期化時の指定（オプショナル・デフォルトのPHYSICAL_IN_XかPHYSICAL_IN_Z）に依存します。

c2c FFTインターフェイスは十分に簡潔な形をしていますが、実数のみを利用する場合はよりコンパクトな形式になります：


call decomp_2d_fft_3d(in, out)

ここでinは実数配列、outは複素配列で、順変換が適用されます。逆変換は、inが複素配列、outが実数配列の場合に計算されます。

入力が実数の場合、複素数の出力はエルミート冗長性、すなわち互いに複素共役の出力を含みます。これを利用して、FFTアルゴリズムは通常、c2cより倍速く、メモリーを半分で済ませつつ、r2cとc2rを計算できます。しかしながら、データ構造がより複雑になるという欠点もあります。サイズnx×ny×nzの3D実数入力データに対しては、複素出力配列サイズは(nx/2+1)×ny×nzに出来ます（Fortranの場合です。C/C++ではメモリーパターンが異なるため、最後の次元が半分になります。また、Zペンシル入力では、出力の最後の次元が約半分になります：nx×ny×(nz/2+1)。ここで、整数割り算は切り捨て処理をします）。複素出力を2Dペンシルに分散させるには、セクション4.2で記述したインターフェイスか、あるいは以下のユーティリティールーチンを用いるかどちらかで実行できます：


call decomp_2d_fft_get_dims(start,end,size)

ここで、これら3つの引数は全て3要素の1D配列であり、呼び出し側の返り値は、現在のプロセッサーのサブ領域の最初のインデックス、最後のインデックスおよびサイズです。これは、当初のメイン領域分割ライブラリで定義されたstart/end/size変数と良く似ています。

ここで、XペンシルとZペンシルから得られた複素出力配列は、同じ情報を含むものではないことに注意してください。ですが、エルミート冗長性を考慮すれば、いかなる物理的情報も失われず、実数入力は、複素出力から対応する逆変換によって完全に回復可能です。

最後に以下のFFTインターフェイスによってメモリーをクリアします：


call decomp_2d_fft_finalize

もし必要であれば、同じアプリケーションの最後のファイナライズ後でも、FFTインターフェイスの再初期化は可能です。FFTインターフェイスを試すには、ライブラリに付属のサンプルアプリケーションを試すことをお勧めします。

7 FFT性能

並列FFTライブラリの性能は、基礎となる1DFFTの計算効率と転置アルゴリズムの通信効率で測ることが出来ます。以下の表は、FFTWの3DFFTインターフェイスを用いたシリアル実行に対する、このライブラリの速度向上を示しています。HECToRフェーズ2aでの実行時間を、 c2c順変換とFFTW_ESTIMATEでプランニングされた全ての変換について示しています。

Data size N³	Serial FFTW		Parallel 2DECOMP&FFT
Data size N³	Planning	Execution	16 cores	64 cores	256 cores
64³	0.359	0.00509	0.00222	-	-
128³	1.98	0.0525	0.0223	0.00576	0.00397
256³	8.03	0.551	0.179	0.0505	0.0138
512³	37.5	5.38	1.74	0.536	0.249
1024³	-	-	-	4.59	1.27
2048³	-	-	-	-	17.9

通信コスト要因により、シリアルライブラリに対してそれほど大きな速度実行が示されていません(256コアで20-40倍)。

しかしながら、並列ライブラリは、より大きな問題をより効率的に解くことが出来ています。

特に、小さなコア数(16,64)では、問題サイズが8倍になる度に、計算時間は8-10倍になり、基礎となるシリアルライブラリの傾向に良く追随しています。

FFTインターフェイスの大規模並列ベンチマークを、 HECToRとJaguar（本調査は、National Center for Computational Sciences at Oak Ridge National Laboratory の資源を用い、契約DE-AC05-00OR22725の元、Office of Science of the Department of Energy のサポートを受けました）において、8192³の問題サイズまで実行しました。

図4に示す結果は、乱雑信号の順変換と逆変換の両方の計算時間を示しています。

基盤のFFTエンジンはACML FFT(バージョン4.3)です。全てのケースにおいて、元の信号は逆変換後にマシン精度で再現されており、ライブラリの良い検証となっています。

HECToRフェーズ2aのクアッドコア上で16384コアまで用い、各計算は3回行って最も速い値を記録しました。ベンチマーク作業時に最も高速なマシンであるJaguar上では、131072コアを用いた最大規模のテストを実施しました。実行性能は、通信が支配するアプリケーションにとっては、特にシステムの混雑さにより、大きく変化します。

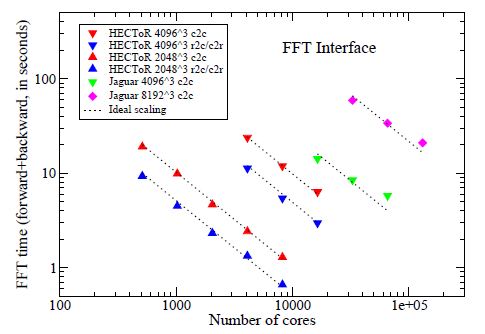
図4：FFTインターフェイスのスケール性能

FFTインターフェイスは、実行したすべてのテストにおいて、HECToR上でほぼ完全にスケールしています。期待通りに、r2c/c2r変換はc2c変換より2倍速いです。

Jaguar上では、大きなコア数ではふるいませんが、それでも効率は81%あります。特に16384コアの4096³メッシュでは、Jaguarでの実行時間はHECToRのそれを2倍上回っており、予想外でした。

2つの6コアチップを搭載するハードウェアで検証をしてみました。良好な負荷バランスを保持するには、問題サイズは6の倍数でなくてはならず、今回のテストは当てはまりません。 8192³でも実用的にはかなり大きなサイズですが、100,000コアでの並列には小さすぎます。

HECToRフェーズ2bでもベンチマークを行いました。ハードウェアのアーキテクチャーの差は、異なるスケール性能を示しました。この結果は、共有メモリープログラミングを議論するセクション8で示します。

7.1 より良い性能達成のためのプラクティス

アプリケーション性能は様々な要因から影響を受けます。例えば、ネットワークのハードウェアに因って、MPIライブラリでは特定のメッセージサイズが有利になります。システム環境変数によるチューニングにより、コード性能を向上させることが多くの場合に可能です。このセクションは、2DECOMP&FFTの振る舞いに影響することが知られている性能上の課題について議論します。

グローバル転置や通信のMPI_ALLTOALLタイプは、大きなネットワークバンド幅を要求することが知られています。よって、大規模アプリケーションは非飽和ノード上でより高速に実行します(図10を参照してください)。これは、メモリーバンド幅の改善からも生じている可能性があります。しかしながら、これはほとんどのスーパーコンピューターがノード単位でリソースを確保するため、あまり実際的ではありません。セクション8で議論する共有メモリープログラミングが、その解決に役立つでしょう。

2DECOMP&FFT利用時に、2DプロセッサーグリッドP_row×P_colの選択自由度に注意すべきです。ハードウェア、特にネットワークレイアウトに依存して、特定のプロセッサーグリッドは他よりも良い性能を示します。大規模シミュレーション実行前に、こうした課題に対処することが推奨されます。

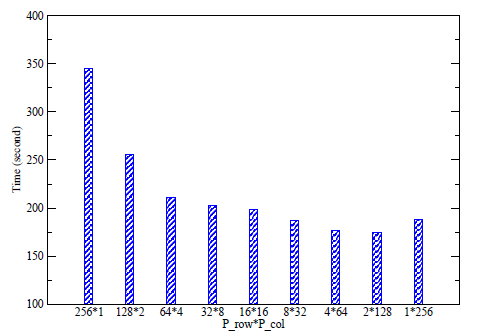
図5：プロセッサーグリッドに対する通信ライブラリの性能

図5は、HECToR上での256MPIランクを用いたテスト結果を示しています。前世代のCray SeaStar2インターコネクト・マシンにおけるこのテストにおいては、P_row<<P_colが最も良いことが解ります。こうした振る舞いには幾つかの理由があります。最初にこのハードウェアは、クアッドコアプロセッサー(4-way SMP)を搭載しています。P_rowが4以下の場合、MPI_ALLTOALLVの半分は完全に物理ノード内で実行されて高速です。第二に、通信ライブラリはijk順に配列を操作しますが、P_rowが小さい場合は(つまり最内側ループカウントnx/P_rowが大きい)コード内の計算部のキャッシュ効率が向上します。

図5に示された振る舞いは、決して代表例であるというわけではありません。事実、この振る舞いは、時間で変化するシステム負荷や、グローバルメッシュのサイズや形、その他の要因に大きく依存しています。このライブラリには自動チューニングアルゴリズムが搭載されており、以下のようにスイッチできます：


call decomp_2d_init(nx,ny,nz,0,0)

領域分割ライブラリを初期化した際に、プロセッサーグリッドが0×0であれば、最良のプロセッサーグリッドを決めるのに自動チューニングアルゴリズムが用いられます。しかしこれは通信コストのみを考慮します。また、計算が支配的なコードにとっては、キャッシュ効率の方が重要です。よって最良のプロセッサーグリッドの決定はユーザーに委ねられています。

8 共有メモリー実装

多くの現代的なスーパーコンピューターは、マルチコアプロセッサーを搭載し、同一ノード上のコアは多くの場合共有メモリーを持ちます。HECToRフェーズ2aが搭載するクアッドコアプロセッサーのコアは、8GBメモリーを共有しています。HECToRフェーズ2bでは、ノード当たり24コアで32GBのメモリーを共有します。

ALLTOALL型の通信では、各MPIランクは、他のMPIランクへ/から、メッセージを送信/受信しなくてはならず、同じ物理ノード上のコアからの通信トラフィックは、そのネットワークインターフェイスで競合することが容易に想像できます。ネットワークバンド幅が十分な場合でさえ、小さいメッセージが多すぎるとネットワークのレイテンシーにより性能は影響を受けます。解決策の一つは、各SMPノード上で送信/受信バッファを共有することです。ノード内の1ランクのみがMPI_ALLTOALL(V)に参加して、より少ない数のより大きなメッセージを用いる事により、通信性能の向上を期待できます。スーパーコンピューターのインターコネクトは、多くの場合、少量の大きなメッセージ操作に最適化されています。

こうした手法は、通信ライブラリ内にブラックボックスとして実装されています。コンパイル時にフラグ'-DSHM'を用いると有効になります。この共有メモリーコードは、多くのUNIXで広く用いられているSystem V内部プロセス通信(IPC)APIを利用しています。2DECOMP&FFTは、2つの独立した共有メモリー手法を実装しています：

最初のバージョンは、Cray社のDavid Tanquerayから提供されました。彼は最初にこのアイデアを分子動力学コードへ適用しました。このコードはプラットフォーム依存情報を用いて共有メモリーパラメーター（どのMPIランクがどのノードに属すか等)を収集します。このため、Crayハードウェアのみでサポートされます。
第二バージョンは、nAGのIan Bushが作成したオープンソースパッケージFreeIPCを用いています。FreeIPCは、基本的にはSystem V IPCのFortranラッパーで、システムに依存しない方法で共有メモリー情報を収集します。よりポータブルな共有メモリーコードを作成することが可能です。

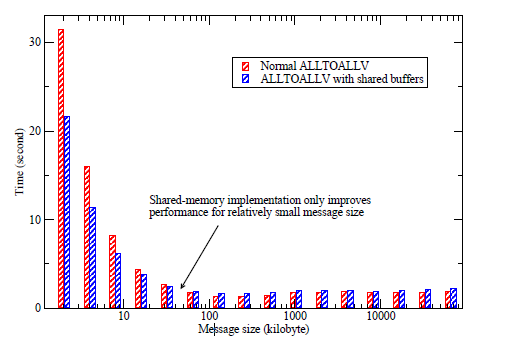
図6：共有メモリーコードの性能

図6は、共有メモリープログラミングでの典型的な利点を表しています。この測定データは、HECToRフェーズ2aにおける256MPIランクを用いた、様々な問題サイズに対する一連のシミュレーション結果を集約したものです。問題サイズが小さい(メッセージサイズが小さい)場合、システム内のデータ量は一定なので、通信ルーチンはより多数呼ばれます。図6は、問題サイズが小さい時、通信セットアップのオーバーヘッドが大きく、共有メモリープログラミングが30％まで通信効率を向上させていることを示しています。問題サイズが大きくなると、共有メモリーの利点は減少します。大きなサイズ(この例では32Kb以上)では、共有メモリーコードは、余分なメモリーコピー操作により遅くなります。

フェーズ2bへアップグレードしたHECToR上で、実アプリケーションでの共有メモリープログラミングの性能を評価しました。新たなGeminiインターコネクトの搭載前に、24コアのノードがHECToRへ導入されました。従来においては、通信が支配的なコードは、古いSeaStarインターコネクトのものよりも多くのネットワークトラフィックを発生していました。図7は、2592³サイズを用いた2DECOMP&FFTによるFFTのベンチマークを示しています。

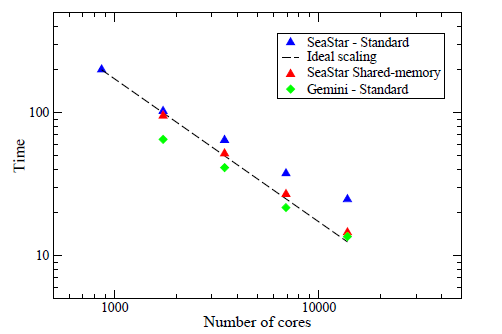
図7：SeaStarおよびGeminiインターコネクトでの並列FFT性能

低速なSeaStarインターコネクトによるスケール性能は、数千コア以上を用いた場合に極めて劣化しています。しかしながら共有メモリーコードは、大きく性能を改善し(場合により40％以上)、全スケールに渡って並列効率90％以上を示しています。新しいGeminiインターコネクトは、ネットワークのバンド幅とレイテンシーを大幅に改善します。結果として、通信が支配的なコードでは大きな性能改善が期待されます。FFTベンチマークは、場合によってほぼ2倍に向上します。しかしながら、Geminiを用いた共有メモリーコードは、ネットワークがメッセージを効率的に素早く処理するので、まったく利点を生かせません(図には示していません)。この場合、共有メモリーバッファーの組み立て/分解に要求される追加のメモリーコピーのために、アプリケーションはスローダウンさせられます。

9 Incompact3Dへの適用

ここまででライブラリ開発が終了し、いよいよCFDアプリケーションへ適用します。本セクションでは、最初にこのプロジェクトの科学的な背景を簡単に説明し、次に、ここで用いられる数値計算アルゴリズムとその並列実装手法を議論し、最後に本プロジェクトによる新しいコードの性能を報告します。

9.1 背景

本プロジェクトの目的は、ユニークな特徴を持つCFDアプリケーションIncompact3Dに対して、HPC技術における最新の開発結果を適用し、乱流の理解に資することです。

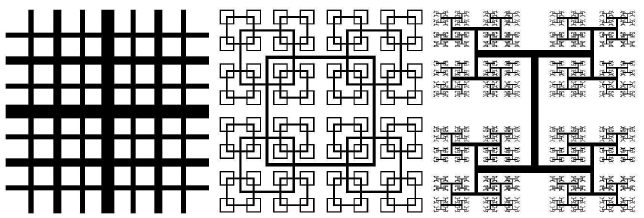
図8：フラクタルグリッドの3タイプ

インペリアル・カレッジ・ロンドンの乱流、混流、流体制御(Turbulence,Mixing and Flow Control)グループの学術協力者は、10年近く最先端のエネルギー問題に取り組んできました。つい最近の彼らの仕事の1例として、マルチスケール/フラクタル形状により生成される乱流という新しい流体コンセプトが有ります。この種の新規の流体コンセプトは、工業用ミキサーや、静粛なエアブレーキ、新しい換気装置や燃焼装置等で有用な、新しい流体ソリューションを提供する可能性を秘めています。インペリアル・カレッジ・ロンドンでは多くの風洞実験が行われています[10,15]。これらの実験結果を補い、背後の物理を理解するためには、このようなマルチスケール流体の高解像度シミュレーションが必要とされます。

最小スケールの乱流渦を解像するには、極めて大規模なシミュレーションが必要です。実際には、メッシュ点数は10億のオーダーが必要になります。そのためには、利用可能なスーパーコンピューターを適切に用いるためのソフトウェアの開発が必要となります。グループのEPSRCからの予算は4百万AUであり、HECToRへは英国乱流コンソーシアムからアクセスするため、高いスケール性能を持ち、リソースを有効に活用するコードを準備することが重要です。

9.2 Incompact3Dの数値計算アルゴリズム

Incompact3Dは、非圧縮性流体の支配方程式を解くCFDアプリケーションです。こうしたアプリケーションの並列化には、多くの場合、開発を必要とする2つの場面があります。一つは、ナビエストークス方程式の空間離散化と近似、二つ目は、質量保存を満足させるための圧力ポアソン方程式の解法です。Incompact3Dアルゴリズムの完全な解説は、Laizet & Lamballais[12]を参照してください。本報告は、このコードの並列化に関係する箇所のみに焦点を当てます。

Incompact3Dは、カルテシアン・メッシ上のナビエストークス方程式の移流項と拡散項の離散化に、6次のコンパクト差分スキームを用います。空間微分と空間補間を行う演算子は、陰的な形式を取ります。例えば、collocated mesh上での一次微分は以下の式で計算されます：

\begin{eqnarray} \alpha f_{i-1}'+f_i'+\alpha f_{i+1}'=a \frac{f_{i+1}-f_{i-1}}{2\Delta x} +b \frac{f_{i+2}-f_{i-2}}{4\Delta x} \tag{1} \end{eqnarray}

この形式は、3つの空間方向全ての各グローバルメッシュ線に沿った三重対角系を解くことになります。並列実装においては、三重対角系は、領域分割ライブラリのグローバル転置ルーチンを用いてローカルメモリーへデータを分散して、内製のシリアル実行ソルバーを用いて解きます。

圧力ポアソン方程式の数値計算アルゴリズムは数多くありますが、繰返し法と直接法の2つのカテゴリーで大まかに分類できます。マルチグリッド法は繰返し法の中で最も効果的で、一方FFTベースのソルバーは最も効率的な直接法です。

ポアソン方程式を解くFFTベースの手法には、2つのタイプがあります。最初のものは、行列分解(matrix decomposition)とも呼ばれ、ポアソン方程式の有限差分離散化を扱うフーリエの方法を用います。通常の中心差分を用いると、3Dポアソン方程式の有限差分離散化は、7重対角系になります。これを解くには、一次元についてフーリエ変換を行って、系を一連の5重対角系へ落とします。更に二番目の次元にフーリエ変換を施すと、一連の3重対角系となって、これを効率的に解くことが出来ることになります。このような方法の数学的定式化は、特に周期系でない場合や異なるメッシュ構成のアプリケーション(スタッガード.vs.collocated mesh)においては、1970年代に確立されており[16,17]、オープンソースFISHPACK[4]ではシリアル実行形式で実装されています。この方法は、2DECOMP&FFTフレームワークに大変にうまく当てはまる形式であり、ローカルメモリー内で一方向毎に1D FFTと3重対角ソルバーを実行すれば良く、データは転置ルーチンを用いて正しく再配置可能です。

Incompact3Dに適用されたポアソンソルバーは、第二の方法で、開発された3D並列FFTライブラリの利点を直接に活用するために、完全なスペクトル解法でポアソン方程式を扱います。アルゴリズムは以下のステップを踏みます：

物理空間での前処理
3D FFT順変換
スペクトル空間での前処理
波数(modified wave numbers)分割によりポアソン方程式を解く
スペクトル空間でのポスト処理
3D FFT逆変換
物理空間でのポスト処理

上記の順方向と逆方向の変換は、標準的なFFTです(非周期境界条件問題も含む)。境界条件に依りますが、前処理とポスト処理のある部分はオプショナルです。数学的詳細は省きますが、前処理とポスト処理には、波数の計算と、標準的なFFTルーチンを用いることの出来る形式へ変換する離散コサイン変換を含みます。

前処理とポスト処理は、local：データの並列分散に関わらず可能で、global：データがメモリー上で全て局所化されている場合に限り可能な(すなわち、計算は特定のペンシル方向で実行される)、両方の場合で実行できます。幸いにも、グローバルケースでは、要求されるデータが無い場合でも、ライブラリのグローバル転置ルーチンはデータの再配置に用いることが出来ます。2D領域分割における順方向および逆方向FFTは、4つのグローバル転置を要求します。物理的な境界条件に依りますが、上記の前処理とポスト処理は、12までのグローバル転置を追加可能です。

9.3 新しいIncompact3Dの性能

元のIncompact3Dは、1Dスラブ領域分割で並列化されていました。これは大規模シミュレーションに大きな制約です。例えば、2048*512*512メッシュのシミュレーションは、512コアまでしかスケールアップできません。HECToRフェーズ1のハードウェアでは、これは、ジョブ投入時間を除いて5012時間、つまり25日の実行時間が掛かります。明らかにこのままでは、より生産的な科学研究を望めません。

新しいIncompact3Dは、2DECOMP&FFTライブラリを用いて完全に書き換えられ、HECToRの1万コアまでスケールしています。その性能評価のために、4096³までのメッシュ点を用意し、HECToR上で16384コア(フェーズ2aの全リソースの72％)までのシミュレーションを実行しました。その結果を図9に示します。

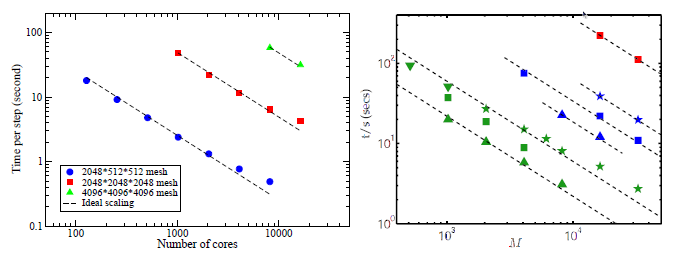
図9：強スケーリング性能。左図： 2DECOMP&FFTを組み込んだIncompact3D。右図：P3DFFTを用いたP.K.Yeung[9]によるスペクトルDNSコード(参考値)

HECToR上での新しいコードの性能は極めて良好です。比較として、P3DFFTを用いたP.K.Yeung[9]によるスペクトルDNSコードも示しています。直接比較が可能なデータは、緑三角で示したスーパーコンピューターFranklin(Cray XT4)のデータで、大変よく似たスケール性を示しています。

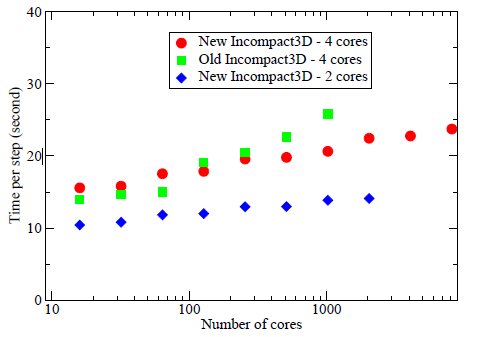
図10：HECToR上のIncompact3Dの弱スケーリング性能

図10は、MPIランク当り4191304メッシュ点を与えた場合の、Incompact3Dの弱スケーリング性能を示しています。HECToRフェーズ2a上での新/旧コードの性能比較が可能です。元のコードは1Dスラブ領域分割で実装されており、小さなコア数では優っています。新しいコード性能は、大きなコア数において元のコードを上回ります。これは通信がMPIタスクのサブセット間のみで行われ、効率が向上していることが要因の一つです。

緩やかな性能向上(1024コアで約20％)に加えて、元のコードでの1D領域分割による制限(1024コアまでしか計算不可)は、新しいコードには当てはまりません。このスケーラビリティ改善は、より大きなシミュレーションをより短い時間で実行可能にして、科学的な成果をより素早く生み出すことが可能になります。

図10はまた、クアッドコアノードの2コアのみを用いた場合は、メモリーとネットワークのバンド幅向上により、30％ほど高速化することを示しています。これが示唆するのは、ノードレベルの他の並列機構を導入すれば、即ちOpenMP並列の利用により、更に性能が向上する可能性がある事です。

10 結論と今後

本プロジェクトを通して、CFDアプリケーションIncompact3Dは、現代的で、ポータブルかつ高スケール性のソフトウェアパッケージへと変更されました。その非常に高い並列性能をHECToR上で実証しました。これにより、超大規模の最先端の乱流シミュレーションが可能となりました。

本プロジェクトの主要な成果の一つが、一般目的の2D領域分割ライブラリと並列FFTインターフェイスをカプセル化した2DECOMP&FFTパッケージの開発です。このパッケージは、多くのアプリケーションにとって有用になるでしょう。現在2DECOMP&FFTは、燃焼コード(DSTAR)、圧縮性DNSコード(Compact3D)、海洋モデリングコード等のアプリケーションに導入されつつあります。

今後のより良いアプリケーションサポートのために、2DECOMP&FFTに対して追加する価値のある機能として、以下のものがあります：

ハロ(halo)セルのサポート：隣接ペンシルに直接にメッセージ送受信をさせることにより、2D領域分割フレームワーク上で陽解法の実装を可能にする。
一般的なデータレイアウトのサポート：現在は入出力データに、ijk順の配列のみをサポートしている。より一般的なデータレイアウトをサポートすることにより、より柔軟で効率的なアプリケーション作成が可能になる。
C/C++言語サポート：最初には、Fortranライブラリの単純なラッパーが可能である。しかし、メモリー操作（例えばMPI_ALLTOALLバッファーのパッキング/アンパッキングなど)の効率性は、メモリーパターン(C言語では行優先、Fortranでは列優先)に強く依存しており、コードのC/C++専用の修正が必要である。

Incompact3Dには、以下の開発が将来的に役立つでしょう：

計算が支配的なコード部分について、OpenMP並列を実装する。
非同期MPI転置演算により計算と通信のオーバーラップを可能にする。
multiple-writerモデルによるMPI-IOを用いて、より洗練された並列I/Oを実装する。

最後になりますが、2DECOMP&FFTライブラリの情報はCrayユーザーグループによる[14]を参照してください。Incompact3Dの他のスーパーコンピューター上の並列性能については、論文誌[13]で紹介されています。

謝辞

このプロジェクトは、nAG Ltd.が運営するHECToRの分散計算科学および工学(CSE)サービスの基に実行されました。英国の国立スーパーコンピューティング・サービスである、HECToR：英国リサーチ・カウンシル・ハイエンド計算サービスは、リサーチ・カウンシルを代行するEPSRCが管理しています。そのミッションは英国学術界の科学および工学の研究支援です。HECToRスーパーコンピューターは、UoE HPCx Ltd.およびnAG Ltd.のCSEサポートサービスにより管理運営されています。

文献

[1]	FFTE website. http://www.ffte.jp/.
[2]	FFTPACK5 website. http://people.sc.fsu.edu/?jburkardt/f_src/fftpack5/fftpack5.html.
[3]	FFTW website. http://www.fftw.org/.
[4]	FISHPACK home page at the netlib repository. http://www.netlib.org/fishpack/.
[5]	Fortran source code of Glassman's algorithm. http://www.jjj.de/fft/glassman-fft.f.
[6]	P3DFFT website. http://www.sdsc.edu/us/resources/p3dfft/.
[7]	PFFT website. http://www-user.tu-chemnitz.de/?mpip/software.php?lang=en.
[8]	Plimpton's parallel FFT package. http://www.sandia.gov/?sjplimp/docs/fft/README.html.
[9]	D. A. Donzis, P. K. Yeung, and D. Pekurovsky. Turbulence simulation on o(10⁴) processors. In TeraGrid'08, June 2008.
[10]	D. Hurst and J.C. Vassilicos. Scalings and decay of fractal-generated turbulence. Physics of Fluids, 19(3), 2007.
[11]	W. E. Ferguson Jr. Simple derivation of Glassman's general N fast fourier transform. Computers & Mathematics with Applications, 8(6):401-411, 1982.
[12]	S. Laizet and E. Lamballais. High-order compact schemes for incompressible flows: A simple and efficient method with quasi-spectral accuracy. Journal of Computational Physics, 228(16):5989-6015, 2009.
[13]	S. Laizet and N. Li. Incompact3d, a powerful tool to tackle turbulence problems with up to 0(10⁵) computational cores. International Journal of Numerical Methods in Fluids, 2010.
[14]	N. Li and S. Laizet. 2DECOMP&FFT - a highly scalable 2D decomposition library and FFT interface. In Cray User Group 2010 conference, May 2010.
[15]	R.E. Seoud and J.C. Vassilicos. Dissipation and decay of fractal-generated turbulence. Physics of Fluids, 19(10), 2007.
[16]	P.N. Swarztrauber. The methods of cyclic reduction, fourier analysis and the FACR algorithm for the discrete solution of Poisson's equation on a rectangle. SIAM Review, 19(3):490-501, 1977.
[17]	R.B. Wilhelmson and J.H. Erickson. Direct solutions for Poisson's equation in three dimensions. Journal of Computational Physics, 25(4):319-331, 1977.

プログラムの高速化・並列化サービスの事例

チューニングレポート：非圧縮性流体/乱流の直接数値シミュレーション（DNS）コードの性能改善