Uwe Naumann, Jacques du Toit*
RWTH Aachen University, Germany,
*Numerical Algorithms Group(nAG)Ltd., UK
(2016年1月掲載)
前半の議論は 数理ファイナンスにおける典型的な数値計算パターンへのアジョイント自動微分ツールの適用(前半部) をご覧ください。
5 アンサンブルとエボリューション
ここで、dco/c++ が我々のテストアプリケーションのメモリー使用率を実質的に削減することを示します。これは、アプリケーション内の特定の構造的な性質を利用することによって行われます。
なお、以下で議論する技法は最適化されたものではありませんが、多くの実務コードにおいてこれらの技法は、大きなメモリーを持つマシン上であっても、テープベースのアジョイントコードの実行には欠かせないテクニックです。
5.1 アンサンブル:モンテカルロ・シミュレーションにおける独立性の利用
ここでセクション 3.1 のモンテカルロ・アプリケーションの一次のアジョイント・バージョンを考えましょう。テープのメモリー要求は何れにせよサンプルパス数に比例します。
dco/c++ による自動アジョイントコード生成では、すぐにメモリーが飽和してしまいます。効率的なシリアル・アジョイントの生成のための独立性(並列性)の利用に関する概念は文献 [Hascoët et al., 2002] で議論されています。
「チェックポイント」は、計算途中のある一点で(ディスクかメモリーのどちらかに)保存されるデータの集合であり、その点から計算を再度開始することを可能にします。モンテカルロ・シミュレーションは通常以下の形式をとります。
\begin{eqnarray} F:(\mathbf{x},\tilde{\mathbf{x}}) \buildrel f_1 \over \longrightarrow (\mathbf{u},\tilde{\mathbf{u}}), \left( \begin{array}{c} (\mathbf{u},\tilde{\mathbf{u}}_1) \buildrel g \over \longrightarrow (\mathbf{v}_1,\tilde{\mathbf{v}}_1) \\ (\mathbf{u},\tilde{\mathbf{u}}_2) \buildrel g \over \longrightarrow (\mathbf{v}_2,\tilde{\mathbf{v}}_2) \\ \vdots \\ (\mathbf{u},\tilde{\mathbf{u}}_N) \buildrel g \over \longrightarrow (\mathbf{v}_N,\tilde{\mathbf{v}}_N) \\ \end{array} \right), (\mathbf{v}_1,\cdots,\mathbf{v}_N,\tilde{\mathbf{v}}_1,\cdots,\tilde{\mathbf{v}}_N) \\ \buildrel f_2 \over \longrightarrow (y,\tilde{\mathbf{y}}). \tag{19} \end{eqnarray}
ここでは g はオイラー-丸山インテグレータ $(12)$ 式で、$\tilde{\mathbf{u}}_i$ はサンプルパス特定のパッシブ入力乱数($f_1$ の $\tilde{\mathbf{u}}$ を含みます)です。出力 $\mathbf{v}_i$ は $N$ 個のサンプルパスを表し、$f_2$ はペイオフ関数です。
テープのサイズ爆発はgを$N$回評価することから生じます。よってフォワード実行では、g の評価結果をテープに記録すべきではありません。これを行うには、$f_1$ の出力 $(\mathbf{u},\tilde{\mathbf{u}})$ のチェックポイントを作成し、g を計算するのに dco/c++ アジョイントを用いず、通常の浮動小数点データ型(例えば double)を用いる外部関数 g_make_gap を使います。こうして g の各評価においてテープ内にギャップを効率的に作ることが出来ます。このプロセスは図2に示されています。関数 g_make_gap の i 番目の呼出しを考えましょう。ここで外部関数オブジェクト(EFO)が要求され、EFO にアクティブ入力が登録されて、この EFO は double 型の値 $\mathbf{u}'$ が登録されます(パッシブ入力 $\tilde{\mathbf{u}}$ も double 型でチェックポイントに保存されます)。
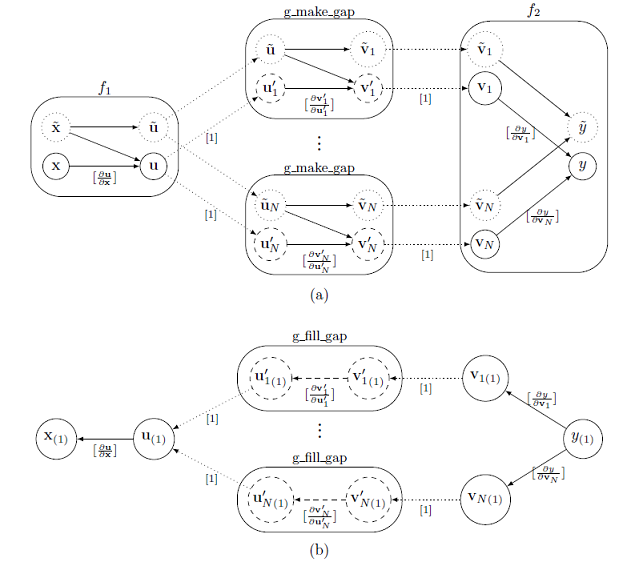
図2:セクション 5.1 で議論したアジョイント・アンサンブル。図 $(a)$ はフォワード実行(記録)を示しています。計算のアクティブ部分(実線の円)はテープです。図 $(b)$ はアジョイント計算を示しています。矢印は偏微分でラベルされています(ゼロを除きます)。点線矢印はテープから外部関数へ(その逆も)の代入です。
添え字 i の意味は逆向きのパスの考察で明らかになります:全ての $\mathbf{u}_i'$ が $\mathbf{u}$ の(パッシブ)値に等しいことに注意しましょう。g_make_gap は、g を計算した後は、EFO へ $(\mathbf{v}_i',\tilde{\mathbf{v}_i})$ を登録し、EFO は $\mathbf{v}_i'$ を新しい dco/c++ アジョイント型(アクティブ出力のみが dco/c++ 型へ変換されます)$\mathbf{v}_i$ へ挿入し、それらがテープに登録されます。よって、式 $(19)$ での g のアクティブ出力 $\mathbf{v}_i'$ は double 型で、$f_2$ の $\mathbf{v}_i$ は dco/c++ の一次アジョイント型です。結果的に、$f_1$ と $f_2$ の値は、g の呼出しが無い間はテープに記録されます。
g_make_gap の呼出し毎に同じチェックポイント $(\mathbf{u},\tilde{\mathbf{u}})$ が生成されます。これで問題はありませんが、十分ではありません。さらに改善する方法はこのレポートに付属のコードで示されています。
与えられた入力アジョイント $y_{(1)}$ に対するテープの解釈(図2$(b)$ で示したように)を始めます。テープ・インタープリターは、$i=1,…,N$ に関して下記のアジョイント全てを計算します。
\begin{eqnarray} \mathbf{v}_{i(1)}:=\mathbf{v}_{i(1)}+\frac{\partial y}{\partial \mathbf{v}_{i}}^T \cdot y_{(1)} =\frac{\partial y}{\partial \mathbf{v}_{i}}^T \cdot y_{(1)}. \tag{20} \\ \end{eqnarray}
ここで、等号は $\mathbf{v}_{i(1)}$ がゼロに初期化された後に成立します。テープ中の各ギャップで、インタープリターはユーザー定義アジョイント関数 g_fill_gap を呼び出し、下記の式を計算します。
\begin{eqnarray} \mathbf{u}_{(1)}:=\mathbf{u}_{(1)}+\frac{\partial \mathbf{v}_i'}{\partial \mathbf{u}}^T \cdot \mathbf{v}_{i(1)}' =\mathbf{u}_{(1)}+\frac{\partial \mathbf{v}_i}{\partial \mathbf{u}}^T \cdot \mathbf{v}_{i(1)}. \tag{21} \\ \end{eqnarray}
ここで、等号は $\mathbf{v}_i$が$\mathbf{v}_i'$ から代入で生成された後に成立します。これを行う最も簡便なやり方は dco/c++ を用いる事です。チェックポイントがリストアされ、値 $\mathbf{u}_i'$ は新しい dco/c++ 一次アジョイントデータ型 $\mathbf{u}_i$ へ挿入されて、g が計算され(概念的に新規の)テープへ記録されます。このテープは入力アジョイント $\mathbf{v}_{i(1)}$ でシードされ、解釈されて、ローカルなアジョイント $\mathbf{u}_{i(1)}$ を生成して、総和計算 $\mathbf{u}_{(1)}:=\mathbf{u}_{(1)}+\mathbf{u}_{i(1)}$ へ加算されます。全ギャップに対して一度これが行われると、インタープリターはアジョイント $\mathbf{x}_{(1)}:=\mathbf{x}_{(1)}+ \frac{\partial \mathbf{u}}{\partial \mathbf{x}}^T \cdot \mathbf{u}_{(1)}$ を計算出来ることになり、アジョイント計算が完了します。
上述の方法は一度に一個のギャップのみを埋めます。g に関する計算が相互に独立であるため、ギャップは並列に埋めることが出来て、並列アジョイント計算が可能となります。ここで示したチェックポイント・スキームは、メモリーの代わりに演算を用いる手法です:各サンプルパスは、アジョイント計算を完了させるのに 2 回計算されます。
表1は、ディスク・スワッピングを用いずに 3GB のメモリーのみで計算した場合の、中心有限差分に対する、$N=10000$ と $M=360$ での mc/a1 と mc/a1s_ensemble の、ピークのメモリー容量と経過時間の比較を示しています。チェックポイントを用いない場合(mc/a1s)は $n \geq 22$ のグラジェントサイズでは非現実的な値になってしまいます。並列性を考慮した mc/a1s_ensemble では、マシン精度内で全グラジェント計算に対するプライマル関数が、$\mathcal{R} \lt 10$ というコストでアジョイント計算が可能です。
| $n$ | mc/primal | mc/cfd | mc/a1s | mc/a1s_ensemble | $\mathcal{R}$ |
| 10 | 0.3s | 6.1s | 1.8s (2GB) | 1.3s (1.9MB) | 4.3 |
| 22 | 0.4s | 15.7s | - (>3GB) | 2.3s (2.2MB) | 5.7 |
| 34 | 0.5s | 29.0s | - (>3GB) | 3.0s (2.5MB) | 6.0 |
| 62 | 0.7s | 80.9s | - (>3GB) | 5.1s (3.2MB) | 7.3 |
| 142 | 1.5s | 423.5s | - (>3GB) | 12.4s (5.1MB) | 8.3 |
| 222 | 2.3s | 1010.7s | - (>3GB) | 24.4s (7.1MB) | 10.6 |
表1:セクション 3.1 のモンテカルロ・カーネルに対する、dco/c++ 一次アジョイントコードと中心有限差分のグラジェントサイズnに関する実行時間とメモリー容量。通常のアジョイントは $n \geq 22$ の場合にメモリー要求が多すぎて実行不可能でした。相対的な計算コスト $\mathcal{R}$ は mc/a1s_ensemble に関する値が示されています。理論的には $\mathcal{R}$ は定数ですが、コンパイラ・オプションや、メモリー階層/キャッシュサイズや、プライマルコードの最適化レベル等に拠り変化します。
表2は、有限差分(前進、中心)により計算されたグラジェントと AD によるものとを比較した表です。最初のグラジェント $(i=0)$ が最も精度が良く、最後のもの $(i=4)$ が最も低くなっており、 中間のものは有限差分のグラジェント精度の中間的な値になっています。これは最小の問題 $(n=10)$ に対する結果です。
| $i$ | mc/ffd | mc/cfd | mc/t1s | mc/a1s_ensemble |
| 0 | 0.982097033091 | 0.982097084181 | 0.982097083159485 | 0.982097083159484 |
| 7 | -0.0716705322265 | -0.071666955947 | -0.0716660568246482 | -0.0716660568246484 |
| 4 | 0.346174240112 | 0.346131324768 | 0.346126820239318 | 0.346126820239324 |
表2:$n=10$ でのモンテカルロ・コードに対する前進、中心有限差分とADによるグラジェント精度の例。最初の行がベストケース(相対誤差が約 $1.0e^{-8}$)で、最終行がワーストケース(相対誤差が約 $6.0e^{-5}$)、中間の行が代表値(相対誤差が約 $2.0e^{-5}$)です。これら有限差分値は実際の計算において出現するものよりも良い値になっています。
5.2 エボリューション:複数チェックポイントによるメモリー制御
エボリューションはシリアル・ループを意味し、反復法がその典型例です。セクション 3.2 で議論した放物型 PDE では、連立方程式の反復解法によりペイオフが時間に逆行して進む場合に生じます。これは以下のように表現できます。
\begin{eqnarray} F:(\mathbf{x},\tilde{\mathbf{x}}) \buildrel f_1 \over \longrightarrow (\mathbf{u_0},\tilde{\mathbf{u_0}}) \buildrel g \over \longrightarrow … \buildrel g \over \longrightarrow (\mathbf{u_N},\tilde{\mathbf{u_N}}) \buildrel f_2 \over \longrightarrow (y,\tilde{\mathbf{y}}). \tag{22} \\ \end{eqnarray}
ここで、各 g は連立方程式の解を表します(一般に $(22)$ 式の各 g は、互いに異なります。しかしながら簡単のためセクション 3.2 のクランク-ニコルソン・ソルバーに対応する場合を示してあります)。以前に示したように、いずれにせよテープのメモリーは時間ステップ数 N に比例します。前のセクションで議論したアンサンブルとエボリューションの違いは、アンサンブルにおいては各関数 g が同じアクティブ入力 $\mathbf{u}$ から開始され、$(22)$ 式での繰り返し毎のそのアクティブ出力が次の繰り返しのアクティブ入力になることです。よって、前のセクションのアイデアを正確に適用でき、$i=0,…N-1$ の各繰り返しの最初の値 $(\mathbf{u_i},\tilde{\mathbf{u_i}}$ をチェックポイントとすることが出来ます。この状況を図3に示しました。
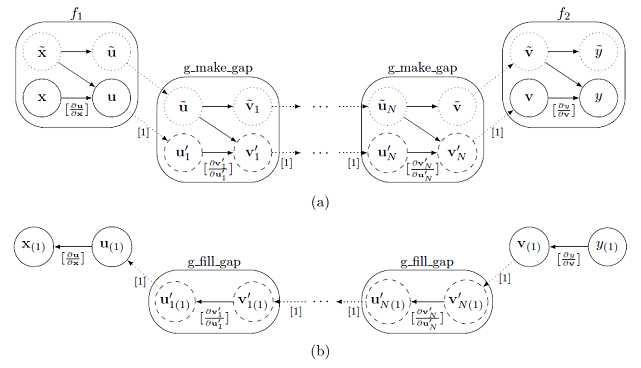
図3:セクション 5.2 で議論されたアジョイント・エボリューション。実線と点線については以前と同等な意味です。図 $(a)$ はフォワード(記録)実行を示し、図 $(b)$ はアジョイント計算を示します。一般に各関数 g_make_gap は場合により異なりますが、ここで議論した PDE ソルバーにおいては全て同じです。
関数 g は、各々のテープ内にギャップが存在するため、'受動的に'(すなわち dco/c++ データ型を用いずに)実行されます。テープがアジョイントを実行するように解釈されたときは、以前と同等の計算を行います。最初に $f_2$ のアジョイント $\mathbf{u_{N(1)}}$ が計算されます。次に $(\mathbf{u_{N-1}},\tilde{\mathbf{u_{N-1)}}})$ のチェックポイントが復元され、新しい dco/c++ 一次アジョイントコードへ挿入されます。最後の N 番目の繰り返しはアクティブに実行され、テープは $\mathbf{u_{N(1)}}$ でシードされ、アジョイント $\mathbf{u_{N-1(1)}}$ が計算されます。そして、$(\mathbf{u_{N-2}},\tilde{\mathbf{u_{N-2)}}})$ のチェックポイントが復元され、同様に続きます。これはペイオフのアジョイント $\mathbf{u_{0(1)}}$ が計算されるまで繰り返され、その後テープの解釈は完了します。
前のセクションで示したように、各チェックポイントは余分な計算をしますが、メモリー容量はセーブされます。もし一回の繰り返しでのメモリー使用量が小さければ、繰り返しの 10 回や 20 回単位でチェックポイントを実施すればよいでしょう。チェックポイント機能は多くの文献で研究されてきました。与えられたメモリーの上限に関して、チェックポイントで置き換えることによりアジョイントのコストを最小化する問題は、NP 完全問題として知られています [Naumann, 2008, Naumann, 2009]。繰り返し数があらかじめ分かっている場合は、二項式チェックポイント法がこの問題を解くことが出来ます [Griewank, 1992]。保存されたチェックポイントから計算の一部を再計算する時のその並行性を利用した、並列アプローチが開発されてきました [Lehmann and Walther, 2002]。
pde/a1s_checkpointing のサンプルコードは、一次アジョイント AD に対して等間隔なチェックポイントを実装するために外部関数インターフェイスを利用したものです。表3は、ディスク・スワッピングを用いずに 3GB のメモリーのみで計算した場合の、中心有限差分に対する、$N=10000$ と $M=360$ での pde/a1s と pde/a1s_checkpointing のピークのメモリー容量と経過時間の比較を示しています。
| $n$ | pde/primal | pde/cfd | pde/a1s | pde/a1s_checkpointing | $\mathcal{R}$ |
| 10 | 0.3s | 6.5s | - (>3GB) | 5.2s (205MB) | 17.3 |
| 22 | 0.5s | 19.6s | - (>3GB) | 8.3s (370MB) | 16.6 |
| 34 | 0.6s | 37.7s | - (>3GB) | 11.6s (535MB) | 19.3 |
| 62 | 1.0s | 119.5s | - (>3GB) | 18.7s (919MB) | 18.7 |
| 142 | 2.6s | 741.2s | - (>3GB) | 39s (2GB) | 15.0 |
| 222 | 4.1s | 1857.3s | - (>3GB) | 60s (3GB) | 14.6 |
表3:プライマルコードとチェックポイント付き一次アジョイントコードと中心有限差分の、グラジェントサイズ n に関する実行時間とメモリー容量。チェックポイントは等間隔(10 回毎)に設定されています。通常のアジョイントは最も小さい問題サイズにおいてもメモリーをオーバーしています。相対的な計算コスト $\mathcal{R}$ は pde/a1s_checkpointing に関する値が示されています。前と同様に、理論的な相対計算コストは定数ですが、コンピュータアーキテクチャやソフトウェア特性に拠り変化します。
通常の(自動)アプローチ(pde/a1s)では、チェックポイントがない場合、全てのグラジェントサイズにおいてメモリー要求が大きすぎます。Pde/a1s_checkpointing における繰り返し 10 回毎の等間隔チェックポイントを用いると、マシン精度内でプライマル関数が、$\mathcal{R}$ がほぼ 15 のコストでアジョイント計算が可能です。文献 [Griewank and Walther, 2000] の resolve のような、最適化された(二項式)チェックポイントを実装した場合には、さらなる改善が期待できます。
AD と比較した有限差分の精度は、表2で示したものと類似した結果になります。
6 その他の話題
6.1 特定の領域に対するアジョイント AD 組込み関数
これまで見てきたように、dco/c++ の外部関数インターフェイスは、プライマル関数とユーザー定義アジョイント関数との関係を定義することが出来ます。これにより、特定の領域における最先端の関数に対して、高度に最適化されたアジョイント・バージョン(例えば、手書きのコードやある AAD ソース変換ツールを用いて手動で最適化した出力コード)を用いる事が可能になります。これをうまく使いこなすためには、これら関数のプライマル実装は、開発や最適化やテストのオーバーヘッドが繰り返しの利用に見合うように、中長期にわたって安定な状態を維持する必要があります。ユーザー定義 dco/c++ 組込み関数全体は、アジョイントによる感度解析や最適化に対する高度にモジュール化したソフトウェア工学的アプローチを援用することで構築されます。
6.2 有限差分とソース非公開ライブラリ
あるファイナンス問題においては、非連続性および/あるいは微分不可能な関数を扱わねばならない場合が生じます。その定義から、これらは古典的な考え方においては微分不能です。有限差分は、このような関数に対する一般化された感度情報の形式を得るための選択肢の一つです。このアプローチはもはや正確な微分の範疇ではありませんが、この一般化された感度情報を、上述したようにユーザー定義アジョイント関数を通して統合することは可能です。こうした手法のミックスが数学的に理に適っているかどうかは、ユーザーの判断に任せられています。非連続性や非平滑性に対する別のアプローチとして、スムーシングがあります。プライマルモデルに対するその連続微分可能な近似形は、dco/c++ で微分可能なものとなります。
有限差分はまた、ソース非公開ライブラリの取り扱いを可能にします。一般にADを行う際は明らかに、関連する全ソースコードが必須です。ソースコードの一部が非公開の場合、それらは有限差分を用いれば扱うことが可能です。nAG ライブラリ(www.nag.com から入手可能です)は現状では、dco/c++で完全に統合された唯一の商用数学ライブラリです。つまり、dco/c++ は nAG ライブラリ内の関数群を組込み関数として扱い、それらの正確な tangent やアジョイントを計算することが出来ます。すなわち、nAG のコンポーネントを用いるプログラムを、あたかも全てのソースコードにアクセスできるかのように扱うことが出来ます。
6.3 (直接法)線形ソルバー
下記のような直接法の線形ソルバーの計算およびメモリーコストの削減において重要なことは、数学上の線形システムとして解析的なアジョイントをシンボリックに導くことを考えることです。
\begin{eqnarray} A \cdot s=b \tag{23} \end{eqnarray}
この線形システムを、ある補助的なスカラー入力変数 $z \in \mathbb{R}$ の関数(多変数関数に拡張するのは容易です)として考えましょう。$(23)$ を微分すると、$\frac{\partial A}{\partial z} \cdot s+A \cdot \frac{\partial s}{\partial z }= \frac{\partial b}{\partial z }$ となります。$s^{(1)}= \frac{\partial s}{\partial z }$ とすれば下記のように書けます(例えば [Giles, 2008] を参照してください)。
\begin{eqnarray} A \cdot s^{(1)}=b^{(1)}- A^{(1)} \cdot s \tag{24} \end{eqnarray}
ここで、$A^{(1)}=\frac{\partial A}{\partial z}、b^{(1)}=\frac{\partial b}{\partial z}$ は、A と b の z に関する偏微分(入力)です。tangent モード AD では z に関する解sの微分は、$A^{(1)}、b^{(1)}$ が用意できれば(例えば $A=A(z),b=b(z)$ に対して tangent モードを dco/c++ で適用して得る)、$(24)$ を解くことによって得られます。
同様の論法で、$(23)$ の与えられた入力アジョイント $s_{(1)}$ に対するアジョイント $A_{(1)}、b_{(1)}$ が下記の式を満たすことが示されます。
\begin{eqnarray} A^T \cdot b_{(1)} && = && \ s_{(1)} \\ A_{(1)} \ && = && \ -b_{(1)} \cdot s^T \tag{25} \end{eqnarray}
ここで、入力アジョイントは、例えば dco/c++ を適用した、プライマルコード中の線形システムの解計算にアジョイントモードを適用して得られます。以上の結果から、二つのことが解ります。
- ・線形システム $(23)$ の tangent $s^{(1)}$ とアジョイント $A_{(1)}、b_{(1)}$ に対して解析的な式 $(24)$ があるため、これらを計算するのに AD を用いる必要はありません。
- ・プライマルコードで計算されるAの分解は、方程式を解くために $(24)$ と $(25)$ で再使用される。
よって、微分計算コストは、微分が行列・ベクトル積で計算されるため、例えば密な行列ならば $O(n^3)$ から $O(n^2)$ へ大幅に減少させることが出来ます。アジョイント計算においては同様のことがテープのメモリー要求に対して生じます:もし AD が $(23)$ のアジョイント計算に用いられる場合は、$O(n^3)$ のメモリーが要求されます。ですが今の場合は、A の分解と解のベクトル s が保存対象であり、これらは $O(n^2)$ の規模となります。
上記のアプローチは、線形システムの正確なプライマル解 s へ適用可能なものと考えています。この要求は、繰り返し法では満足されるものではありません。何故なら、その感度に要求される精度を得るには、プライマル解のより高い精度が要求されるからです。例えば、10 や 12 の有効桁を確保するには、アプリケーションで検証が必要とされますが、倍精度のアジョイント計算で十分でしょう。
セクション 3.2 のクランクーニコルソン法における計算およびメモリーコスト削減効果は、行列 A が三重対角でスパースなケースではより抑えられることになります。よって、本レポートの PDE カーネルにはあまり役立たないという理由から、ソースコード・アーカイブには上述の実装は含めておりません。ただし、ファイナンス問題において、大きな密行列を扱う、PIDE や最近接相関行列計算や内部点最適化法などは存在します、が多くはありません。
6.4 求根問題
パラメータ付き非線形方程式システム $F(\mathbf{x},\mathbf{\lambda})=0$ について、解 $\mathbf{x}=\mathbf{x}*$ においてパラメータ $\lambda$ に関して微分すると以下の式を得ます。
\begin{eqnarray} \frac{dF}{d\mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) =\frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) +\frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda}) \cdot \frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}=0 \end{eqnarray}
書き直すと、
\begin{eqnarray} \frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}} =-\frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})^{-1} \cdot \frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) \tag{26} \end{eqnarray}
下記の方向微分は、
\begin{eqnarray} \mathbf{x}^{(1)} =\frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}} \cdot \mathbf{\lambda}^{(1)} =-\frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})^{-1} \cdot \frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) \cdot \mathbf{\lambda}^{(1)} \tag{27} \end{eqnarray}
次の線形システムの解です。
\begin{eqnarray} \frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda}) \cdot \mathbf{x}^{(1)} =-\frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) \cdot \mathbf{\lambda}^{(1)} \tag{28} \end{eqnarray}
ここで右辺は $F$ の一回の tangent モード計算で得ることが出来ます。$(28)$ を直接解くには $n×n$ のヤコビアン $\frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})$ が必要ですが、そのスパース性を利用すべく tangent モードで計算します。
$(26)$ の転置は、$\left(\frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}\right)^T=-\left(\frac{\partial F}{\partial \mathbf{\lambda}}\right)^T \cdot \left(\frac{\partial F}{\partial \mathbf{x}}\right)^{-T}$ である事から、以下のように書くことが出来ます。
\begin{eqnarray} \mathbf{\lambda}_{(1)}:= \mathbf{\lambda}_{(1)} + \left(\frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}\right)^T \cdot \mathbf{x}_{(1)} =\mathbf{\lambda}_{(1)} -\frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda})^T \cdot \frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})^{-T} \cdot \mathbf{x}_{(1)} \tag{29} \end{eqnarray}
結果としてアジョイントソルバーは下記の線形システムを解く必要があります。
\begin{eqnarray} \frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})^T \cdot \mathbf{z} =-\mathbf{x}_{(1)} \tag{30} \end{eqnarray}
これは下記の解 $\mathbf{z}$ でシードされた $F$ の 1 回のアジョイントモデル計算によるものです。
\begin{eqnarray} \lambda_{(1)}= \lambda_{(1)} +\frac{\partial F}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda})^T \cdot \mathbf{z}. \end{eqnarray}
このアプローチは非線形システムの正確なプライマル解が可能であることを前提にしています。再度になりますが、アジョイントの望ましい精度を得るには、このプライマル解のより高い精度が必要となります。
6.5 最適化問題
制約なし最適化問題は一次の最適条件 $\frac{\partial F}{\partial \mathbf{x}}(\mathbf{x},\mathbf{\lambda})=0$ に対する求根問題として扱うことが可能です。解 $\mathbf{x}=\mathbf{x}^*$ においてパラメータ $\lambda$ に関して微分すると以下の式を得ます。
\begin{eqnarray} \frac{\partial}{\partial \mathbf{\lambda}} \frac{dF}{d\mathbf{x}}(\mathbf{x},\mathbf{\lambda}) = \frac{\partial^2 F}{\partial \mathbf{\lambda}\partial \mathbf{x}} (\mathbf{x},\mathbf{\lambda}) +\frac{\partial^2 F}{\partial \mathbf{x}^2}(\mathbf{x},\mathbf{\lambda}) \cdot \frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) =0 \end{eqnarray}
よって下記式を得ます。
\begin{eqnarray} \frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) =-\frac{\partial^2 F}{\partial \mathbf{x}^2}(\mathbf{x},\mathbf{\lambda})^{-1} \cdot \frac{\partial^2 F}{\partial \mathbf{\lambda} \partial \mathbf{x}} (\mathbf{x},\mathbf{\lambda}) \tag{31} \end{eqnarray}
前回と同様に方向微分 $\mathbf{x}^{(1)}=\frac{\partial \mathbf{x}}{\partial \mathbf{\lambda} }\cdot \mathbf{\lambda}^{(1)}$ から下記の線形システムが導かれます。
\begin{eqnarray} -\frac{\partial^2 F}{\partial \mathbf{x}^2}(\mathbf{x},\mathbf{\lambda}) \cdot \mathbf{x}^{(1)} =\frac{\partial^2 F}{\partial \mathbf{\lambda} \partial \mathbf{x}} (\mathbf{x},\mathbf{\lambda}) \cdot \mathbf{\lambda}^{(1)} \tag{32} \end{eqnarray}
ここで右辺は $F$ の一回の 2 次のアジョイントモード計算で得ることが出来ます。$(32)$ を直接解く場合は $n×n$ のヘッシアン $\frac{\partial^2 F}{\partial \mathbf{x}^2}(\mathbf{x},\mathbf{\lambda}) $ が必要となりますが、ここで、スパース性を利用するために二次のアジョイントADを用いる事が出来ます。
$(31)$ の転置は、$\left(\frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}\right)^T=-\left(\frac{\partial^2 F}{\partial \mathbf{\lambda} \partial \mathbf{x}}\right)^T \cdot \left(\frac{\partial^2 F}{\partial \mathbf{x}^2}\right)^{-T}$ であるから、以下のように一次アジョイントモデルとして書くことが出来ます。
\begin{eqnarray} \mathbf{\lambda}_{(1)}:= \mathbf{\lambda}_{(1)} + \frac{\partial \mathbf{x}}{\partial \mathbf{\lambda}}(\mathbf{x},\mathbf{\lambda}) ^T \cdot \mathbf{x}_{(1)} =\mathbf{\lambda}_{(1)} -\frac{\partial^2 F}{\partial \mathbf{\lambda}\partial \mathbf{x}} (\mathbf{x},\mathbf{\lambda})^T \cdot \frac{\partial^2 F}{\partial \mathbf{x}^2}(\mathbf{x},\mathbf{\lambda})^{-T} \cdot \mathbf{x}_{(1)} \end{eqnarray}
$\mathbf{\lambda}_{(1)}$ の計算には $\frac{\partial^2 F}{\partial \mathbf{x}^2}^T \cdot \mathbf{z}=-\mathbf{x}_{(1)}$ を解くことになり、これは下記式を計算する解 $z$ での $F$ の二次のアジョイントモデルを一回呼び出して得ることが出来ます。
\begin{eqnarray} \lambda_{(1)}= \lambda_{(1)} +\frac{\partial^2 F}{\partial \mathbf{\lambda}\partial \mathbf{x}} (\mathbf{x},\mathbf{\lambda})^T \cdot \mathbf{z}. \end{eqnarray}
キャリブレーションの観点からのこの方法の議論は [Henrard, 2014] を参考にしてください。制約付き最適化問題の一般化が、KKT(Karush-Kuhn-Tucker)システムをセクション 6 に従って取り扱うと自然に導かれます。
| $n$ | mc/socfd | mc/t2s_t1s | mc/t2s_a1s | mc/t2s_a1s_ensemble |
| 10 | 6s | 4s | 2s (316MB) | 2s (0.5MB) |
| 22 | 35s | 23s | 8s (778MB) | 8s (1.0MB) |
| 34 | 98s | 66s | 18s (1.2GB) | 18s (1.5MB) |
| 62 | 8min | 5.2min | 62s (2.3GB) | 53s (2.5MB) |
| 142 | 2.4hrs | 52min | - (>3GB) | 5.3min (5.7GB) |
| 222 | 6.1hrs | 3.2hrs | - (>3GB) | 13.8min (8.7GB) |
表4:モンテカルロ・コードの全ヘッシアン計算の、グラジェントサイズ $n$ に関する実行時間とメモリー容量。二次の中央差分を、フォワード AD と、ネイティブなアジョイントベース AD と、チェックポイント・アジョイントコードと比較しています。有限差分計算の計測を基本にして、$N=1000$ のサンプルパスのみを測定しました。
6.6 局所ヤコビアンの事前評価
以下の関数に対してアジョイント計算を考えましょう。
\begin{eqnarray} F:(\mathbf{x},\tilde{\mathbf{x}}) \buildrel f_1 \over \longrightarrow (\mathbf{u},\tilde{\mathbf{u}}) \buildrel g \over \longrightarrow (\mathbf{v},\tilde{\mathbf{v}}) \buildrel f_2 \over \longrightarrow (y,\tilde{\mathbf{y}}). \tag{33} \\ \end{eqnarray}
ここで、$\mathbf{u} \in \mathbb{R}^n, \mathbf{v} \in \mathbb{R}^m $、そのヤコビアンは $\nabla g \in \mathbb{R}^{n \times m} $ です。行列 $\nabla g$ の保存に必要な最大のメモリー量は、多くの場合、テープ g に必要とされる量、特に計算が多く含まれている場合は、かなり少なくなります。しかしもしテープ $f_2$ にも大きなメモリーが必要となった場合には、メモリーオーバーになってしまう可能性が高いです。この場合に、もし g のヤコビアンがフォワード計算(例えば、アジョイントモードで dco/c++ を用いて、あるいはもしアジョイントコスト $\mathcal{R}$ に対して $\mathcal{R}・m$ が $n$ より大きい場合には tangent モードを用いて)中に事前に局所的に計算されているならば、メモリーは開放され、g のテープ中にギャップを生成することが出来て、利用が可能です。テープが解釈される時には、そのギャップは保存された行列を用いた計算 $\mathbf{u}_{(1)}:=\mathbf{u}_{(1)}+(\nabla g)^T \cdot \mathbf{v}_{(1)}$ により埋めることが出来ます。
ここで $F$ のアクティブ出力が、ベクトル $\mathbf{y} \in \mathbb{R}^p$ である場合を考えましょう。ヤコビアン $\nabla F$ は行列で、$F$ のアジョイントモデルは $\mathbf{x}_{(1)}:=\mathbf{x}_{(1)}+(\nabla F)^T \cdot \mathbf{y}_{(1)}$ です。全ヤコビアンを計算するには、$\mathbf{y}_{(1)}$ を $\mathbb{R}^p$ のカルテシアン基底ベクトルでシードします。つまりヤコビアンの各列に一度づつ、テープ・インタープリターを $p$ 回実行することを意味します。ヤコビアン $\nabla g$ を事前に計算しておくことにより、テープ・インタープリターの計算毎の再計算を避けることが出来て、ヤコビアン計算のコストを削減することが出来ます。
7 結論
アジョイント AD は極めて強力な数値計算技術です。C++ コード開発においてそれを用いる場合は、メモリーと計算コストを操作でき、アジョイント計算全体に渡ってユーザーに十分な制御を可能にする、柔軟性のあるツールが必要となります。
dco/c++ は特にこのような制御を可能にするよう設計されており、本レポート(および付録のコード)は数理ファイナンスの範囲ですが、こうしたコストを制御するテクニックを紹介しています。
ここで紹介したツールとテクニックは、xVA 感度計算、ポートフォリオ最適化、キャリブレーション、ヘッジ・ポートフォリオなど、ファイナンス数学全体を通して、最適なメモリー容量を保ちつつ適用可能です。
セクション 2 で示したように、高次の微分も概念的な困難さはありません。dco/c++ 型の再帰的なインスタンス化により、任意の次数の微分が可能であり、アジョイントモデルにはメモリー問題がありますが、本レポートで示したテクニックを用いればそれらを制御することが可能です。
完全を期すために、表4では、セクション 3.1 におけるモンテカルロ・コードの全ヘッシアン計算における実行時間とメモリー容量を示しました。
dco/c++ は GPU のようなアクセラレータと共用が可能です。例えば [Du Toit et al., 2014] や [Gremse et al., 2014] をご覧ください。
Intel Xeon Phi での dco/c++ 利用については公開されたレポートはありませんが、dco/c++ は intel の LEO をサポートし、Xeon Phi で tangent およびアジョイントモードを利用することは可能です。
アジョイント計算の困難さに関する一般的な議論はこのプラットフォームにも同様にあてはまります。tangent モードにおける dco/c++ は、CUDA でフルサポートされており、すぐに利用可能です。
アジョイントモードの dco/c++ はこれらデバイス上で動作可能ですが、メモリーが限られ、メモリーアクセスを協調的に行うには注意深さが必要なため、効果的に用いるには困難が伴います。
さらに共有変数のアジョイントの更新には競合状況が生じます。ホストとデバイス上のテープは、メモリーとして分離されており、そのデバイス上の各スレッドは利用可能な跳梁よりも大きなメモリー容量のテープを必要とします。
これらの理由により、アジョイントモードの dco/c++ はそのデバイス上でなく、コードのホスト部分で用いられる場合が多いです。
デバイス上では2つの主要なポイントがあります。最初に、[Gremse et al., 2014] で示された医療イメージ再構成の考察で設定されたように、単一の問題領域にフォーカスを絞り込むことです。
この領域のアルゴリズムは、線形代数演算にブレークダウン可能である場合が多くみられます。
これらは(セクション 6.3 のような)解析的なものでなく、出来上がった GPU カーネルは(セクション 6.1 のように)dco/c++ の組込み関数として組み込むことが可能です。
このことにより、デバイスのコードは(カーネルは小さく、行列・ベクトル積が多いため)メモリーバンド幅の制限で特徴づけられることになりますが、このアプローチは対象とする問題領域において割とうまく行きます。
しかしながら、多くの数値計算カーネルが簡単に線形代数演算に分解できない数理ファイナンス領域においては、それほど簡単にはうまく行きません。効率的なコードは、[Du Toit et al., 2014] で示されたように手動でアジョイントカーネルを高速化することで達成されます。
しかしながらプライマルコードが頻繁に変化する場合には、このやり方は理想的ではありません。ソース変換ツール(例えば [Hasco ë t and Pascual, 2013] )は、コードを扱うことができるように提供されています。
その他に dco/c++ 型を C++11 の特徴を用いて拡張するオプションがあり、コンパイル時に C++11 コンパイラを用いれば、straight-line code(分岐無かつ関数呼出しがないコードに対して)のブロックのアジョイントを生成することが可能です。
よってコードブロックに対してテープへの書き込みがないものを生成可能です。これは現在進行形の研究トピックであり、アクセラレータ向けの効率的なアジョイントカーネルの生成を容易にするでしょう。
8 謝辞
著者らは、AD ツールが大銀行の定量分析ライブラリへ適用した際に直面する課題の完全な理解、および本レポートを導いた多くの示唆と有用な議論に対して、シニア定量アナリストの Claudia Yastremiz に感謝の意を表します。
参考文献
| [Andersen and Brotherton-Ratcliffe, 2000] Andersen, L. B. G. and Brotherton-Ratcliffe, R.$(2000)$. The equity option volatility smile: an implicit finite difference approach. Journal of Computational Finance. |
| [Bischof et al., 2008] Bischof, C., Bücker, M., Hovland, P., Naumann, U., and Utke, J., editors $(2008)$. Advances in Automatic Differentiation, volume 64 of Lecture Notes in Computational Science and Engineering. Springer. |
| [Borsdorf and Higham, 2010] Borsdorf, R. and Higham, N. J. $(2010)$. A preconditioned (Newton) algorithm for the nearest correlation matrix. IMA Journal of Numerical Analysis 30(1). |
| [Bücker et al., 2005] Bücker, M., Corliss, G., Hovland, P., Naumann, U., and Norris, B., editors $(2005)$. Automatic Differentiation: Applications, Theory, and Implementations, volume 50 of Lecture Notes in Computational Science and Engineering. Springer. |
| [Capriotti, 2011] Capriotti, L. $(2011)$. Fast greeks by algorithmic differentiation. Journal of Computational Finance, 14(3). |
| [Cont and Tankov, 2004] Cont, R. and Tankov, P. $(2004)$. Financial Modelling with Jump Processes. Chapman & Hall. |
| [Du Toit et al., 2014] Du Toit, J., Lotz, J., and Naumann, U. $(2014)$. Algorithmic differentiation of a gpu accelerated application. nAG Technical Report No. TR2/14. |
| [Forth et al., 2012] Forth, S., Hovland, P., Phipps, E., Utke, J., and Walther, A., editors $(2012)$. |
| Recent Advances in Algorithmic Differentiation, volume 87 of Lecture Notes in Computational Science and Engineering. Springer. |
| [Gamma et al., 1995] Gamma, E., Helm, R., Johnson, R., and Vlissides, J. $(1995)$. Design Patterns. Addison-Wesley. |
| [Gebremedhin et al., 2005] Gebremedhin, A., F., M., and Pothen, A. $(2005)$. What color is your Jacobian? Graph coloring for computing derivatives. SIAM Review, 47(4):629-705. |
| [Giles, 2008] Giles, M. $(2008)$. Collected matrix derivative results for forward and reverse mode algorithmic differentiation. In [Bischof et al., 2008], pages 35-44. Springer. |
| [Giles and Glasserman, 2006] Giles, M. and Glasserman, P. $(2006)$. Smoking adjoints: Fast monte carlo greeks. Risk, 19:88-92. |
| [Gremse et al., 2014] Gremse, F., Theek, B., Kunjachan, S., Lederle, W., Pardo, A., Barth, S., Lammers, T., Naumann, U., and Kiessling, F. $(2014)$. Absorption reconstruction improves biodistribution assessment of uorescent nanoprobes using hybrid uorescence-mediated tomography. Theranostics 4, 960-971. |
| [Griewank, 1992] Griewank, A. $(1992)$. Achieving logarithmic growth of temporal and spatial complexity in reverse automatic differentiation. Optimization Methods and Software, 1:35-54. |
| [Griewank, 2013] Griewank, A. $(2013)$. On stable piecewise linearization and generalized algorithmic differentiation. Optimization Methods and Software, 28(6):1139-1178. |
| [Griewank and Walter, 2008] Griewank, A. and Walter, A. $(2008)$. Evaluating Derivatives. Principles and Techniques of Algorithmic Differentiation (2. Edition). SIAM, Philadelphia. |
| [Griewank and Walther, 2000] Griewank, A. and Walther, A. $(2000)$. Algorithm 799: Revolve: An implementation of checkpoint for the reverse or adjoint mode of computational differentiation. ACM Transactions on Mathematical Software, 26(1):19-45. Also appeared as Technical University of Dresden, Technical Report IOKOMO-04-1997. |
| [Hascoët et al., 2002] Hascoët, L., Fidanova, S., and Held, C. $(2002)$. Adjoining independent computations. In Corliss, G., Faure, C., Griewank, A., Hascoët, L., and Naumann, U., editors, Automatic Differentiation of Algorithms: From Simulation to Optimization, Computer and Information Science, chapter 35, pages 299-304. Springer, New York, NY. |
| [Hascoët and Pascual, 2013] Hascoët, L. and Pascual, V. $(2013)$. The Tapenade automatic differentiation tool: Principles, model, and speciffcation. ACM Transactions on Mathematical Software, 39(3):20:1-20:43. |
| [Henrard, 2014] Henrard, M. $(2014)$. Adjoint algorithmic differentiation: calibration and implicit function theorem. Journal of Computational Finance. To appear. |
| [Lehmann and Walther, 2002] Lehmann, U. and Walther, A. $(2002)$. The implementation and testing of time-minimal and resource-optimal parallel reversal schedules. In Sloot, P. M. A., Tan, C. J. K., Dongarra, J. J., and Hoekstra, A. G., editors, Computational Science - ICCS 2002, Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, April 21{24, 2002. Part II, volume 2330 of Lecture Notes in Computer Science, pages 1049-1058, Berlin. Springer. |
| [Matache et al., 2004] Matache, A. M., von Petersdorff, T., and Schwab, C. $(2004)$. Fast deterministic pricing of options on levy-driven assets. M2AN. Mathematical Modelling and Numerical Analysis, 38. |
| [Naumann, 2008] Naumann, U. $(2008)$. Call tree reversal is NP-complete. In [Bischof et al., 2008], pages 13-22. Springer. |
| [Naumann, 2009] Naumann, U. $(2009)$. DAG reversal is NP-complete. Journal of Discrete Algorithms, 7:402-410. |
| [Naumann, 2012] Naumann, U. $(2012)$. The Art of Differentiating Computer Programs. An Introduction to Algorithmic Differentiation. Number 24 in Software, Environments, and Tools. SIAM. |
| [Naumann and Lotz, 2012] Naumann, U. and Lotz, J. $(2012)$. Algorithmic differentiation of numerical methods: Tangent-linear and adjoint direct solvers for systems of linear equations. Technical Report AIB-2012-10, LuFG Inf. 12, RWTH Aachen. |
| [Qi and Sun, 2006] Qi, H. and Sun, D. $(2006)$. A quadratically convergent Newton method for computing the nearest correlation matrix. SIAM Journal of Matrix Analysis and Applications 29(2). |
| [Schanen et al., 2012] Schanen, M., Foerster, M., Lotz, J., Leppkes, K., and Naumann, U. $(2012)$. Adjoining hybrid parallel code. In et al., B. T., editor, Proceedings of the Fifth International Conference on Engineering Computational Technology, pages 1-19. Civil-Comp Press. |
| [Schmitz et al., 2011] Schmitz, M., Hannemann-Tamas, R., Gendler, B., Förster, M., Marquardt, W., and Naumann, U. $(2011)$. Software for higher-order sensitivity analysis of parametric DAEs. SNE, 22(3-4):163-168. |
| [Voßbeck et al., 2008] Voßbeck, M., Giering, R., and Kaminski, T. $(2008)$. Development and first applications of TAC++. In [Bischof et al., 2008], pages 187-197. Springer. |
| [W. Xu, 2014] W. Xu, X. Chen, T. C. $(2014)$. The effcient application of automatic differentiation for computing gradients in financial applications. Journal of Computational Finance. To appear. |
