概要
本サンプルはFortran言語によりLAPACKルーチンZHPGVを利用するサンプルプログラムです。
一般化エルミート固有値問題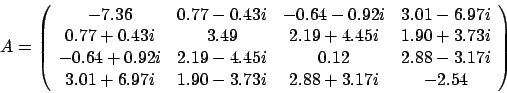
及び
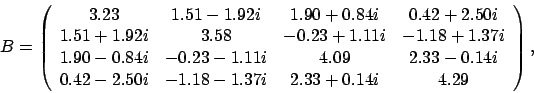
ZHPGVDの例題プログラムは一般化対称固有値問題 ![]() の解き方を示します。
の解き方を示します。
入力データ
(本ルーチンの詳細はZHPGV のマニュアルページを参照)| このデータをダウンロード |
ZHPGV Example Program Data
4 :Value of N
(-7.36, 0.00) ( 0.77, -0.43) (-0.64, -0.92) ( 3.01, -6.97)
( 3.49, 0.00) ( 2.19, 4.45) ( 1.90, 3.73)
( 0.12, 0.00) ( 2.88, -3.17)
(-2.54, 0.00) :End of matrix A
( 3.23, 0.00) ( 1.51, -1.92) ( 1.90, 0.84) ( 0.42, 2.50)
( 3.58, 0.00) (-0.23, 1.11) (-1.18, 1.37)
( 4.09, 0.00) ( 2.33, -0.14)
( 4.29, 0.00) :End of matrix B
出力結果
(本ルーチンの詳細はZHPGV のマニュアルページを参照)| この出力例をダウンロード |
ZHPGV Example Program Results
Eigenvalues
-5.9990 -2.9936 0.5047 3.9990
Estimate of reciprocal condition number for B
2.5E-03
Error estimates for the eigenvalues
6.7E-13 4.1E-13 1.9E-13 5.0E-13
ソースコード
(本ルーチンの詳細はZHPGV のマニュアルページを参照)※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。
| このソースコードをダウンロード |
Program zhpgv_example
! ZHPGV Example Program Text
! Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com
! .. Use Statements ..
Use lapack_interfaces, Only: zhpgv, zlanhp, ztpcon
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Parameters ..
Integer, Parameter :: nin = 5, nout = 6
Character (1), Parameter :: uplo = 'U'
! .. Local Scalars ..
Real (Kind=dp) :: anorm, bnorm, eps, rcond, rcondb, t1, t2
Integer :: i, info, j, n
! .. Local Arrays ..
Complex (Kind=dp), Allocatable :: ap(:), bp(:), work(:)
Complex (Kind=dp) :: dummy(1, 1)
Real (Kind=dp), Allocatable :: eerbnd(:), rwork(:), w(:)
! .. Intrinsic Procedures ..
Intrinsic :: abs, epsilon
! .. Executable Statements ..
Write (nout, *) 'ZHPGV Example Program Results'
Write (nout, *)
! Skip heading in data file
Read (nin, *)
Read (nin, *) n
Allocate (ap((n*(n+1))/2), bp((n*(n+1))/2), work(2*n), eerbnd(n), rwork( &
3*n-2), w(n))
! Read the upper or lower triangular parts of the matrices A and
! B from data file
If (uplo=='U') Then
Read (nin, *)((ap(i+(j*(j-1))/2),j=i,n), i=1, n)
Read (nin, *)((bp(i+(j*(j-1))/2),j=i,n), i=1, n)
Else If (uplo=='L') Then
Read (nin, *)((ap(i+((2*n-j)*(j-1))/2),j=1,i), i=1, n)
Read (nin, *)((bp(i+((2*n-j)*(j-1))/2),j=1,i), i=1, n)
End If
! Compute the one-norms of the symmetric matrices A and B
anorm = zlanhp('One norm', uplo, n, ap, rwork)
bnorm = zlanhp('One norm', uplo, n, bp, rwork)
! Solve the generalized symmetric eigenvalue problem
! A*x = lambda*B*x (ITYPE = 1)
Call zhpgv(1, 'No vectors', uplo, n, ap, bp, w, dummy, 1, work, rwork, &
info)
If (info==0) Then
! Print solution
Write (nout, *) 'Eigenvalues'
Write (nout, 100) w(1:n)
! Call ZTPCON to estimate the reciprocal condition
! number of the Cholesky factor of B. Note that:
! cond(B) = 1/RCOND**2
Call ztpcon('One norm', uplo, 'Non-unit', n, bp, rcond, work, rwork, &
info)
! Print the reciprocal condition number of B
rcondb = rcond**2
Write (nout, *)
Write (nout, *) 'Estimate of reciprocal condition number for B'
Write (nout, 110) rcondb
! Get the machine precision, EPS, and if RCONDB is not less
! than EPS**2, compute error estimates for the eigenvalues
eps = epsilon(1.0E0_dp)
If (rcond>=eps) Then
t1 = eps/rcondb
t2 = anorm/bnorm
Do i = 1, n
eerbnd(i) = t1*(t2+abs(w(i)))
End Do
! Print the approximate error bounds for the eigenvalues
Write (nout, *)
Write (nout, *) 'Error estimates for the eigenvalues'
Write (nout, 110) eerbnd(1:n)
Else
Write (nout, *)
Write (nout, *) 'B is very ill-conditioned, error ', &
'estimates have not been computed'
End If
Else If (info>n .And. info<=2*n) Then
i = info - n
Write (nout, 120) 'The leading minor of order ', i, &
' of B is not positive definite'
Else
Write (nout, 130) 'Failure in ZHPGV. INFO =', info
End If
100 Format (3X, (6F11.4))
110 Format (4X, 1P, 6E11.1)
120 Format (1X, A, I4, A)
130 Format (1X, A, I4)
End Program
