概要
本サンプルはFortran言語によりLAPACKルーチンZHEEVを利用するサンプルプログラムです。
エルミート行列のすべての固有値と固有ベクトルを求めます。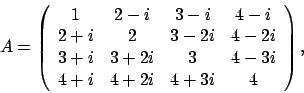
計算された固有値と固有ベクトルの誤差限界近似値も合わせて求めます。
入力データ
(本ルーチンの詳細はZHEEV のマニュアルページを参照)| このデータをダウンロード |
ZHEEV Example Program Data
4 :Value of N
(1.0, 0.0) (2.0, -1.0) (3.0, -1.0) (4.0, -1.0)
(2.0, 0.0) (3.0, -2.0) (4.0, -2.0)
(3.0, 0.0) (4.0, -3.0)
(4.0, 0.0) :End of matrix A
出力結果
(本ルーチンの詳細はZHEEV のマニュアルページを参照)| この出力例をダウンロード |
ZHEEV Example Program Results
Eigenvalues
-4.2443 -0.6886 1.1412 13.7916
Eigenvectors
1 2 3 4
1 -0.3839 0.6470 0.0179 0.3309
-0.2941 0.0000 -0.4453 -0.1986
2 -0.4512 -0.4984 0.5706 0.3728
0.1102 -0.1130 -0.0000 -0.2419
3 0.0263 0.2949 -0.1530 0.4870
0.4857 0.3165 0.5273 -0.1938
4 0.5602 -0.2241 -0.2118 0.6155
0.0000 -0.2878 -0.3598 0.0000
Error estimate for the eigenvalues
3.1E-15
Error estimates for the eigenvectors
8.6E-16 1.7E-15 1.7E-15 2.4E-16
ソースコード
(本ルーチンの詳細はZHEEV のマニュアルページを参照)※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。
| このソースコードをダウンロード |
Program zheev_example
! ZHEEV Example Program Text
! Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com
! .. Use Statements ..
Use blas_interfaces, Only: zscal
Use lapack_example_aux, Only: nagf_file_print_matrix_complex_gen
Use lapack_interfaces, Only: ddisna, zheev
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Parameters ..
Integer, Parameter :: nb = 64, nin = 5, nout = 6
! .. Local Scalars ..
Real (Kind=dp) :: eerrbd, eps
Integer :: i, ifail, info, k, lda, lwork, n
! .. Local Arrays ..
Complex (Kind=dp), Allocatable :: a(:, :), work(:)
Complex (Kind=dp) :: dummy(1)
Real (Kind=dp), Allocatable :: rcondz(:), rwork(:), w(:), zerrbd(:)
! .. Intrinsic Procedures ..
Intrinsic :: abs, cmplx, conjg, epsilon, max, maxloc, nint, real
! .. Executable Statements ..
Write (nout, *) 'ZHEEV Example Program Results'
Write (nout, *)
! Skip heading in data file
Read (nin, *)
Read (nin, *) n
lda = n
Allocate (a(lda,n), rcondz(n), rwork(3*n-2), w(n), zerrbd(n))
! Use routine workspace query to get optimal workspace.
lwork = -1
Call zheev('Vectors', 'Upper', n, a, lda, w, dummy, lwork, rwork, info)
! Make sure that there is enough workspace for block size nb.
lwork = max((nb+1)*n, nint(real(dummy(1))))
Allocate (work(lwork))
! Read the upper triangular part of the matrix A from data file
Read (nin, *)(a(i,i:n), i=1, n)
! Solve the Hermitian eigenvalue problem
Call zheev('Vectors', 'Upper', n, a, lda, w, work, lwork, rwork, info)
If (info==0) Then
! Print solution
Write (nout, *) 'Eigenvalues'
Write (nout, 100) w(1:n)
Write (nout, *)
Flush (nout)
! Normalize the eigenvectors so that the element of largest absolute
! value is real.
Do i = 1, n
rwork(1:n) = abs(a(1:n,i))
k = maxloc(rwork(1:n), 1)
Call zscal(n, conjg(a(k,i))/cmplx(abs(a(k,i)),kind=dp), a(1,i), 1)
End Do
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
Call nagf_file_print_matrix_complex_gen('General', ' ', n, n, a, lda, &
'Eigenvectors', ifail)
! Get the machine precision, EPS and compute the approximate
! error bound for the computed eigenvalues. Note that for
! the 2-norm, max( abs(W(i)) ) = norm(A), and since the
! eigenvalues are returned in descending order
! max( abs(W(i)) ) = max( abs(W(1)), abs(W(n)))
eps = epsilon(1.0E0_dp)
eerrbd = eps*max(abs(w(1)), abs(w(n)))
! Call DDISNA to estimate reciprocal condition
! numbers for the eigenvectors
Call ddisna('Eigenvectors', n, n, w, rcondz, info)
! Compute the error estimates for the eigenvectors
Do i = 1, n
zerrbd(i) = eerrbd/rcondz(i)
End Do
! Print the approximate error bounds for the eigenvalues
! and vectors
Write (nout, *)
Write (nout, *) 'Error estimate for the eigenvalues'
Write (nout, 110) eerrbd
Write (nout, *)
Write (nout, *) 'Error estimates for the eigenvectors'
Write (nout, 110) zerrbd(1:n)
Else
Write (nout, 120) 'Failure in ZHEEV. INFO =', info
End If
100 Format (3X, (8F8.4))
110 Format (4X, 1P, 6E11.1)
120 Format (1X, A, I4)
End Program
