概要
本サンプルはFortran言語によりLAPACKルーチンDGGSVDを利用するサンプルプログラムです。
一般化特異値分解を行います。ここで
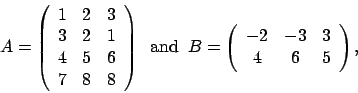
この例題プログラムは ![]() であることを想定していますが、そうでない場合には若干のコード変更が必要です。
であることを想定していますが、そうでない場合には若干のコード変更が必要です。
入力データ
(本ルーチンの詳細はDGGSVD のマニュアルページを参照)| このデータをダウンロード |
DGGSVD Example Program Data 4 3 2 :Values of M, N and P 1.0 2.0 3.0 3.0 2.0 1.0 4.0 5.0 6.0 7.0 8.0 8.0 :End of matrix A -2.0 -3.0 3.0 4.0 6.0 5.0 :End of matrix B
出力結果
(本ルーチンの詳細はDGGSVD のマニュアルページを参照)| この出力例をダウンロード |
DGGSVD Example Program Results
Number of infinite generalized singular values (K)
1
Number of finite generalized singular values (L)
2
Numerical rank of (A**T B**T)**T (K+L)
3
Finite generalized singular values
1.3151E+00 8.0185E-02
Orthogonal matrix U
1 2 3 4
1 -1.3484E-01 5.2524E-01 -2.0924E-01 8.1373E-01
2 6.7420E-01 -5.2213E-01 -3.8886E-01 3.4874E-01
3 2.6968E-01 5.2757E-01 -6.5782E-01 -4.6499E-01
4 6.7420E-01 4.1615E-01 6.1014E-01 1.5127E-15
Orthogonal matrix V
1 2
1 3.5539E-01 -9.3472E-01
2 9.3472E-01 3.5539E-01
Orthogonal matrix Q
1 2 3
1 -8.3205E-01 -9.4633E-02 -5.4657E-01
2 5.5470E-01 -1.4195E-01 -8.1985E-01
3 0.0000E+00 -9.8534E-01 1.7060E-01
Nonsingular upper triangular matrix R
1 2 3
1 -2.0569E+00 -9.0121E+00 -9.3705E+00
2 -1.0882E+01 -7.2688E+00
3 -6.0405E+00
Estimate of reciprocal condition number for R
4.2E-02
Error estimate for the generalized singular values
5.3E-15
ソースコード
(本ルーチンの詳細はDGGSVD のマニュアルページを参照)※本サンプルソースコードのご利用手順は「サンプルのコンパイル及び実行方法」をご参照下さい。
| このソースコードをダウンロード |
Program dggsvd_example
! DGGSVD Example Program Text
! Copyright 2017, Numerical Algorithms Group Ltd. http://www.nag.com
! .. Use Statements ..
Use lapack_example_aux, Only: nagf_file_print_matrix_real_gen_comp
Use lapack_interfaces, Only: dggsvd3, dtrcon
Use lapack_precision, Only: dp
! .. Implicit None Statement ..
Implicit None
! .. Parameters ..
Integer, Parameter :: nin = 5, nout = 6
! .. Local Scalars ..
Real (Kind=dp) :: eps, rcond, serrbd
Integer :: i, ifail, info, irank, j, k, l, lda, ldb, ldq, ldu, ldv, &
lwork, m, n, p
! .. Local Arrays ..
Real (Kind=dp), Allocatable :: a(:, :), alpha(:), b(:, :), beta(:), &
q(:, :), u(:, :), v(:, :), work(:)
Integer, Allocatable :: iwork(:)
Character (1) :: clabs(1), rlabs(1)
! .. Intrinsic Procedures ..
Intrinsic :: epsilon
! .. Executable Statements ..
Write (nout, *) 'DGGSVD Example Program Results'
Write (nout, *)
Flush (nout)
! Skip heading in data file
Read (nin, *)
Read (nin, *) m, n, p
lda = m
ldb = p
ldq = n
ldu = m
ldv = p
Allocate (a(lda,n), alpha(n), b(ldb,n), beta(n), q(ldq,n), u(ldu,m), &
v(ldv,p), work(m+3*n), iwork(n))
! Read the m by n matrix A and p by n matrix B from data file
Read (nin, *)(a(i,1:n), i=1, m)
Read (nin, *)(b(i,1:n), i=1, p)
! Compute the generalized singular value decomposition of (A, B)
! (A = U*D1*(0 R)*(Q**T), B = V*D2*(0 R)*(Q**T), m>=n)
lwork = m + 3*n
Call dggsvd3('U', 'V', 'Q', m, n, p, k, l, a, lda, b, ldb, alpha, beta, &
u, ldu, v, ldv, q, ldq, work, lwork, iwork, info)
If (info==0) Then
! Print solution
irank = k + l
Write (nout, *) 'Number of infinite generalized singular values (K)'
Write (nout, 100) k
Write (nout, *) 'Number of finite generalized singular values (L)'
Write (nout, 100) l
Write (nout, *) 'Numerical rank of (A**T B**T)**T (K+L)'
Write (nout, 100) irank
Write (nout, *)
Write (nout, *) 'Finite generalized singular values'
Write (nout, 110)(alpha(j)/beta(j), j=k+1, irank)
Write (nout, *)
Flush (nout)
! ifail: behaviour on error exit
! =0 for hard exit, =1 for quiet-soft, =-1 for noisy-soft
ifail = 0
Call nagf_file_print_matrix_real_gen_comp('General', ' ', m, m, u, &
ldu, '1P,E12.4', 'Orthogonal matrix U', 'Integer', rlabs, 'Integer', &
clabs, 80, 0, ifail)
Write (nout, *)
Flush (nout)
Call nagf_file_print_matrix_real_gen_comp('General', ' ', p, p, v, &
ldv, '1P,E12.4', 'Orthogonal matrix V', 'Integer', rlabs, 'Integer', &
clabs, 80, 0, ifail)
Write (nout, *)
Flush (nout)
Call nagf_file_print_matrix_real_gen_comp('General', ' ', n, n, q, &
ldq, '1P,E12.4', 'Orthogonal matrix Q', 'Integer', rlabs, 'Integer', &
clabs, 80, 0, ifail)
Write (nout, *)
Flush (nout)
Call nagf_file_print_matrix_real_gen_comp('Upper triangular', &
'Non-unit', irank, irank, a(1,n-irank+1), lda, '1P,E12.4', &
'Nonsingular upper triangular matrix R', 'Integer', rlabs, &
'Integer', clabs, 80, 0, ifail)
! Call DTRCON to estimate the reciprocal condition
! number of R
Call dtrcon('Infinity-norm', 'Upper', 'Non-unit', irank, &
a(1,n-irank+1), lda, rcond, work, iwork, info)
Write (nout, *)
Write (nout, *) 'Estimate of reciprocal condition number for R'
Write (nout, 120) rcond
Write (nout, *)
! So long as irank = n, get the machine precision, eps, and
! compute the approximate error bound for the computed
! generalized singular values
If (irank==n) Then
eps = epsilon(1.0E0_dp)
serrbd = eps/rcond
Write (nout, *) 'Error estimate for the generalized singular values'
Write (nout, 120) serrbd
Else
Write (nout, *) '(A**T B**T)**T is not of full rank'
End If
Else
Write (nout, 130) 'Failure in DGGSVD3. INFO =', info
End If
100 Format (1X, I5)
110 Format (3X, 8(1P,E12.4))
120 Format (1X, 1P, E11.1)
130 Format (1X, A, I4)
End Program
